Basile Audoly

Contact info:
audoly[(a)]lmm[.]jussieu[.]fr
Laboratoire de Mécanique des Solides — École Polytechnique —  F-91128 Palaiseau

I am a researcher at the CNRS (directeur de recherches) and Professeur associé à temps partiel, working at LMS/Polytechnique.

misc

  • Our book Elasticity and Geometry is available (B.A. and Y. Pomeau, Oxford University Press, 2010): Table of contents, link to Amazon page, and to editor's page.
  • Discrete Elastic Rods, which has been licensed to Adobe, serves as the foundation for the Bristle Tips feature Adobe Illustrator and Adobe Photoshop (versions CS5 and later).

    teaching

    publications

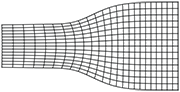
    My research interests are mainly nonlinear mechanics, buckling, rods, plates and shells theories

    Analysis of necking based on a one-dimensional model

    B. Audoly and J. W. Hutchinson. Journal of the Mechanics and Physics of Solids, to appear, 2015.

    Derivation of a one-dimensional model describing the necking of prismatic solids, and analysis of the model. Both nonlinearly elastic materials displaying a maximum load on their traction curve, and elasto-plastic materials are studied.

    [preprint][journal][bib]

    Untangling the mechanics and topology in the frictional response of long overhand elastic knots

    M. K. Jawed, P. Dieleman, B. Audoly, and P. M. Reis. hysical Review Letters, 115:118302, 2015.

    Experiments and theory characterizing the response of overhand knots with many turns, tied in a stiff filament. A first step towards connecting knot topology and mechanics.

    [preprint][journal][bib]

    Liquid ropes: a geometrical model for thin viscous jet instabilities

    P.-T. Brun, B. Audoly, N. Ribe, T. S. Eaves, and J. R. Lister. Physical Review Letters, 114(17):174501, 2015.

    A simple geometrical model describing the complex patterns laid down by a thin viscous jets impacting on a moving surface.

    [preprint][journal][bib]

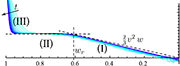
    Dynamic curling of an Elastica: a nonlinear problem in elastodynamics solved by matched asymptotic expansions

    B. Audoly, A. Callan-Jones, and P.-T. Brun. In D. Bigoni, editor, Extremely Deformable Structures, volume 562 of CISM International Centre for Mechanical Sciences, pages 137-155. Springer, 2015.

    A detailed derivation of the solution for the dynamic curling of naturally curved, initially flat Elastica by matched asymptotic expansions, published in short form in Phys. Rev. Lett. (2012).

    [journal][bib]

    Buckling of naturally curved elastic strips: the ribbon model makes a difference

    B. Audoly and K. A. Seffen. Journal of Elasticity, 119(1):293Ð320, 2015.

    Stability analysis for thin elastic strips, based on the ribbon model, using a formulation similar to classical rod theory.

    [preprint][journal][bib]

    Introduction to the elasticity of rods

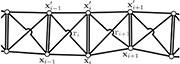
    B. Audoly. In C. Duprat and H. A. Stone, editors, Fluid-Structure Interactions in Low-Reynolds-Number Flows, RSC Soft Matter, chapter 1. RSC publishing, 2015.

    [journal][bib]

    "Wunderlich, meet Kirchhoff": A general and unified description of elastic ribbons and thin rods

    M. A. Dias and B. Audoly. Journal of Elasticity, 119(1):49-66, 2015.

    Wunderlich and Sadowsky models for wide elastic strips fit naturally into the theory of elastic rods.

    [preprint][journal][bib]

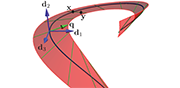
    An introduction to the mechanics of the lasso

    P.-T. Brun, N. M. Ribe, and B. Audoly Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 470(2171):20140512, 2014.

    Wunderlich and Sadowsky models for wide elastic strips fit naturally into the theory of elastic rods.

    [preprint][journal][bib]

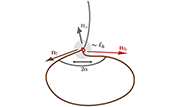
    Furrow constriction in animal cell cytokinesis

    H. Turlier, B. Audoly, J. Prost, and J.-F. Joanny. Biophysical Journal, 106(1):114-123, 2014.

    The mechanics of cell division using a viscous shell model with active stress.

    [preprint][journal][bib]

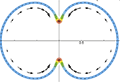
    Shapes of a suspended curly hair

    J. T. Miller, A. Lazarus, B. Audoly, and P. M. Reis. Physical Review Letters, 112:068103, 2014.

    How human hair twists and curls.

    [preprint][journal][bib]

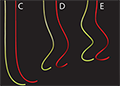
    A non-linear rod model for folded elastic strips

    M. A. Dias and B. Audoly. Journal of the Mechanics and Physics of Solids, 62:57-80, 2014.

    Making origami by folding an elastic ribbon.

    [preprint][journal][bib]

    Solid drops: Large capillary deformations of immersed elastic rods

    S. Mora, C. Maurini, T. Phou, J.-M. Fromental, B. Audoly, and Y. Pomeau. Physical Review Letters, 111:114301, 2013.

    Capillary deformation of a prismatic gel immersed in a fluid (experiments, theory and simulation).

    [preprint][journal][bib]

    A discrete geometric approach for simulating the dynamics of thin viscous threads

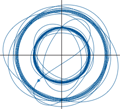
    B. Audoly, N. Clauvelin, P.-T. Brun, M. Bergou, E. Grinspun, and M. Wardetzky. Journal of Computational Physics, 253:18-49, 2013.

    Direct simulations of thin viscous jets including the effect of bending, twisting, inertia and surface tension by a geometric method. Validation on helical coiling and demos of the viscous sewing machine.

    [preprint][journal][bib]

    Capillary buckling of a thin film adhering to a sphere

    J. Hure, and B. Audoly. Journal of the Mechanics and Physics of Solids, 61:450-471, 2013

    Analysis of wavy patterns produced by wrapping a thin film onto a wet sphere.

    [preprint][journal][bib]

    A numerical investigation of the fluid mechanical sewing machine

    P.-T. Brun, N. M. Ribe, and B. Audoly. Physics of fluids, 24(4):043102, 2012

    Numerical simulation and mathematical analysis of the patterns laid down by a thin viscous jet onto a moving belt.

    [preprint][journal][bib]

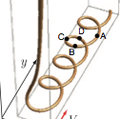
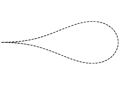
    Self-similar curling of a naturally curved Elastica

    A. C. Callan-Jones, P.-T. Brun, and B. Audoly. Physical Review Letters, 108(17):174302, 2012

    What happens when a circular spring is laid flat on a table and released?

    [preprint][journal][bib]

    Discrete viscous sheets

    C. Batty, A. Uribe, B. Audoly, and E. Grinspun. Transactions on Graphics, 31(4):113:1-7, 2012

    An efficient numerical model for simulating thin viscous sheets.

    [preprint][journal][bib]

    The shape of an elastic loop strongly bent by surface tension: experiments and comparison with theory

    S. Mora, T. Phou, J.-M. Fromental, B. Audoly, and Y. Pomeau. Physical Review Letters E, 86(2):026119, 2012

    Strong deformation of a very flexible elastic wire holding a soap bubble, as a mean to measure surface tension.

    [preprint][journal][bib]

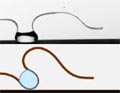
    Instant fabrication and selection of folded structures using drop impact

    A. Antkowiak, B. Audoly, C. Josserand, S. Neukirch, and M. Rivetti. Proceedings of the National Academy of Sciences, 108(26):10400-10404, 2011

    When a drop impacts on a thin target, it gets wrapped in a dynamic sequence. Slightly varying the impact parameters allows for shape selection of the final 3D structure.

    [preprint][journal][bib]

    Linear and non-linear stability of floating viscous sheets

    G. Pfingstag, B. Audoly, and A. Boudaoud. Journal of Fluid Mechanics, 683:112-148, 2011

    Buckling analysis of thin viscous sheets subjected to arbitrary volume or surface forces, with application to the wrinkling of floating sheets

    [preprint][journal][bib]

    Thin viscous sheets with inhomogeneous viscosity

    G. Pfingstag, B. Audoly, and A. Boudaoud. Physics of Fluids, 23(6):063103, 2011

    Derivation of the equation governing thin viscous sheets having spatially inhomogeneous viscosity, with illustrations to necking and wrinkling.

    [preprint][journal][bib]

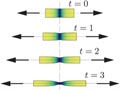
    Localized buckling of a floating Elastica

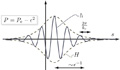
    B. Audoly, Physical Review E (Statistical, Nonlinear, and Soft Matter Physics), 84(1), 2011

    Analysis of the localization of buckling patterns for an Elastica floating on a bath of denser fluid, providing an interpretation of the experimental results of Pocivavsek et al. (Science, 2008)

    [preprint][journal][bib]

    Discrete viscous threads

    M. Bergou, B. Audoly, E. Vouga, M. Wardetzky, and E. Grinspun. Discrete viscous threads. ACM Transactions on Graphics (SIGGRAPH), 29(4):116, 2010

    A discrete model for numerical simulations of the dynamics of thin viscous threads, using dimensional reduction

    [preprint][journal][bib]

    Elasticity and geometry: from hair curls to the nonlinear response of shells (book)

    B. Audoly and Y. Pomeau. Oxford University Press, 600 pages, july 2010

    A book on the nonlinear elasticity of rods, plates and shells.

    [Table of contents][Amazon's page][editor's page][bib]

    Matched asymptotic expansions for twisted elastic knots: a self-contact problem with non-trivial contact topology

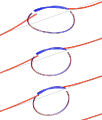
    N. Clauvelin, B. Audoly, and S. Neukirch. J. Mech. Phys. Sol. 57:1623-1656, 2009

    Analytical calculation of the shape of knot on an elastic rod, including the effect of twist. Some experiments are presented.

    [preprint][journal][bib]

    Elasticity and electrostatics of plectonemic DNA

    N. Clauvelin, B. Audoly, and S. Neukirch. Biophysical Journal, 96(9):3716-3723, 2009

    Calculation of loading curves of single-molecule DNA under twist, including electrostatic interactions. Comparison with experiments are shown.

    [preprint][journal][bib]

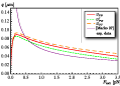
    Mechanical response of plectonemic DNA: An analytical solution

    N. Clauvelin, B. Audoly, and S. Neukirch. Macromolecules 41(12):4479-4483, 2008

    A mechanical model for interpreting the loading curves of single-molecule DNA experiments under twist. Interactions are described by a hard-core potentiel.

    [preprint][journal][bib]

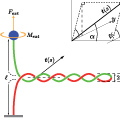
    Discrete elastic rods

    M. Bergou, M. Wardetzky, S. Robinson, B. Audoly, and E. Grinspun. ACM Transactions on Graphics (SIGGRAPH), 27(3):63:1-63:12, 2008

    A discretization of the equations for elastic rods based on ideas from discrete differential geometry

    [MOVIE][preprint][bib]

    Law of spreading of the crest of a breaking wave.

    Y. Pomeau, T. Jamin, M. Le Bars, P. Le Gal, and B. Audoly. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 464(2095):1851-1866, 2008

    How does a breaking wave spread laterally?

    [preprint][journal][bib]

    Buckling of a thin film bound to a compliant substrate (part 1). Formulation, linear stability of cylindrical patterns, secondary bifurcations

    B. Audoly and A. Boudaoud. Journal of the Mechanics and Physics of Solids, 56(7):2401–2421, 2008

    Buckling of a stiff film bound to a compliant substrate: analysis near buckling threshold

    [preprint][journal][bib]

    Buckling of a thin film bound to a compliant substrate (part 2). A global scenario for the formation of herringbone pattern

    B. Audoly and A. Boudaoud. Journal of the Mechanics and Physics of Solids, 56(7):2422—2443, 2008.

    —: a simple buckling model for studying the emergence of herringbone patterns

    [preprint][journal][bib]

    Buckling of a thin film bound to a compliant substrate (part 3). Herringbone solutions at large buckling parameter

    B. Audoly and A. Boudaoud. Journal of the Mechanics and Physics of Solids, 56(7):2444—2458, 2008

    —: analytical solutions describing herringbone patterns, based on Miura-ori (origami) construction

    [preprint][journal][bib]

    Elastic knots

    B. Audoly, N. Clauvelin, and S. Neukirch. Physical Review Letters, 99(16):164301, 2007

    The shape of a loose elastic knot

    [preprint][journal][bib]

    Super-helices for predicting the dynamics of natural hair

    F. Bertails, B. Audoly, M.-P. Cani, B. Querleux, F. Leroy, and J.-L. Lévêque. Super-helices for predicting the dynamics of natural hair. In ACM Transactions on Graphics (SIGGRAPH'06), pages 1180–1187, August 2006

    A mechanical model for simulating dynamic hair motion

    [MOVIE][details][preprint][bib]

    Fragmentation of rods by cascading cracks: Why spaghetti does not break in half

    B. Audoly and S. Neukirch. Physical Review Letters, 95(9):095505, 2005

    Title says all

    [MOVIE][details][preprint][journal][bib]

    Cracks in thin sheets: When geometry rules the fracture path

    B. Audoly, P. M. Reis, and B. Roman. Physical Review Letters, 95:025502, 2005

    Try to tear through a plastic sheet using a blunt tool and you'll get nice oscillations

    [MOVIES][details][preprint][journal][bib]

    Predicting natural hair shapes by solving the statics of flexible rods

    F. Bertails, B. Audoly, B. Querleux, F. Leroy, J.-L. Lévêque, and M.-P. Cani. In J. Dingliana and F. Ganovelli, editors, Eurographics (short papers), Dublin (IR). Eurographics, August 2005

    A mechanical model for simulating human hair: static case

    [details][preprint][bib]

    Oscillatory fracture paths in thin elastic sheets

    B. Roman, P. M. Reis, B. Audoly, S. De Villiers, V. Viguie, and D. Vallet. Comptes Rendus Mecanique, 331(12):811–816, 2003

    Cutting through plastic (preliminary model)

    [preprint][journal][bib]

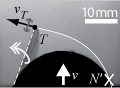
    Self-similar structures near boundaries in strained systems

    B. Audoly and A. Boudaoud. Phys. Rev. Lett., 91(8):086105, Aug 2003

    Try tearing a piece of garbage bag and you'll get fractal wrinkles

    [MOVIE][details][preprint][journal][bib]

    Correlation functions for inhomogeneous magnetic field in random media with application to a dense random pack of spheres

    B. Audoly, P. N. Sen, S. Ryu, and Y. Q. Song. Journal of Magnetic Resonance, 164(1):154–159, 2003

    What can we knot about a porous medium from its NMR signature?

    [journal][bib]

    ‘Ruban à godets’: an elastic model for ripples in plant leaves

    B. Audoly and A. Boudaoud. Comptes Rendus Mecanique, 330(12):831–836, 2002

    Bend a Slinky so that it looks like the edge of a salad leaf

    [preprint][journal][bib]

    The elastic torus: anomalous stiffness of shells with mixed type

    B. Audoly and Y. Pomeau. Comptes Rendus Mecanique, 330(6):425–432, 2002

    Why an elastic torus is really weak

    [preprint][journal][bib]

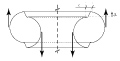
    Secondary buckling patterns of a thin plate under in-plane compression

    B. Audoly, B. Roman, and A. Pocheau. The European Physical Journal B, 27:7–10, 2002

    Nonlinear analysis and experiments on the buckling of an elastic strip

    [preprint][journal][bib]

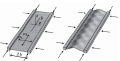
    Asymptotic study of the interfacial crack with friction

    B. Audoly. Journal of the Mechanics and Physics of Solids, 48(9):1851–1864, 2000

    Memory effects and weak singularities in an interfacial crack with Coulomb friction

    [preprint][journal][bib]

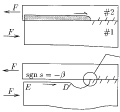
    Mode-dependent toughness and the delamination of compressed thin films

    B. Audoly. Journal of the Mechanics and Physics of Solids, 48(11):2315–2332, 2000

    What sets the size of a delamination blister?

    [preprint][journal][bib]

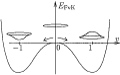
    Réaction-diffusion en écoulement stationnaire rapide

    B. Audoly, H. Berestycki, and Y. Pomeau. Comptes Rendus de l’Academie des Sciences - Series IIB - Mechanics-Physics-Astronomy, 328(3):255–262, 2000

    A very simple model for flame propagation in a turbulent medium

    [preprint][journal][bib]

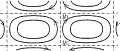
    Elasticity and geometry (Chapter in book)

    B. Audoly and Y. Pomeau. In R. Kaiser and J. Montaldi, editors, Peyresq Lecture Notes on Nonlinear Phenomena, chapter 1, pages 1–35. World Scientific, 2000

    An introduction to the theory of plates

    [book page][bib]

    Stability of straight delamination blisters

    B. Audoly. Physical Review Letters, 83(20):4124–4127, Nov 1999

    Telephone-cord delamination can be understood as the result of a secondary buckling instability

    [preprint][journal][bib]

    Rigidifying curves on surfaces

    B. Audoly. Comptes Rendus de l’Academie des Sciences - Series I - Mathematics, 328(4):313–316, 1999

    A class of curves that can make a surface rigid

    [preprint][journal][bib]

    PhD thesis

    Elasticité et géométrie : de la rigidité des surfaces à la délamination en fil de téléphone

    B. Audoly. PhD thesis, Ecole normale supérieure, University Paris VI, Paris, France, Jan 2000

    [details][pdf][bib]

    • ©B. Audoly, 2008