 |
 |
 |
 |
|
ex: déstablisation de l'oscillateur en rotation. déstablisation de l'oscillateur en rotation.

 3.1 définitions 3.1 définitions
Jusqu'à présent nous nous sommes contentés d'une définition intuitive de la stabilité.
Cette notion nécessite la définition d'une norme (une distance entre le champ perturbé et la

solution de base uB), par exemple on peut prendre:
|
 |
|
||u(x,t)-uB(x,t)|| = maxx[!]Vol |u(x,t)-uB(x,t)| |u(x,t)-uB(x,t)|
|

||u(x,t)-uB(x,t)|| ==
 Vol[!]r/2 (u-uB)2dt Vol[!]r/2 (u-uB)2dt
|
|
 |
|
ou
|
 |
|
- uB sera dit uniformément sera dit uniformément  stable si et seulement si: stable si et seulement si:
 " e>0 ' d>0 / ||u(x,0)-uB(x,0)|| <d => " " e>0 ' d>0 / ||u(x,0)-uB(x,0)|| <d => " t ||u(x,t)-uB(x,t)|| < e t ||u(x,t)-uB(x,t)|| < e
|
 |
|
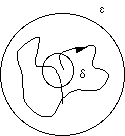
|
 |
|
On reste à l'intérieur de la distance e.

- uB est asymptotiquement est asymptotiquement  stable ssi il est uniformément stable et si stable ssi il est uniformément stable et si
 ' d1>0 ' d1>0 / ||u(x,0)-uB(x,0)|| <d1 / ||u(x,0)-uB(x,0)|| <d1 => limt->[!]|u(x,t)-uB(x,t)|| =0 => limt->[!]|u(x,t)-uB(x,t)|| =0

c2 8 Décembre 1997 8 Décembre 1997 p 6 p 6
|
 |

 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
