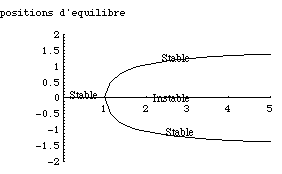
Positions d'équilibre en fonction du paramètre de contrôle (on n'oublie pas +/- pinstable).

Lorsque la valeur du paramètre de contrôle change, la nature de la solution change de même

- si w/w₀<1caractère univoque état/ contrainte

- si w/w₀>1perte d'unicité et de symétrie ( dans les équations la symétrie q-> -q)

N.B.
- au vu de la courbe d'énergie ci-dessus on aurait pu anticiper ces résultats: la cuvette en q=0 se

transforme petit à petit en bosse lorsque w/w₀augmente, la position q=0 devient alors instable.

- la solution q=0 existe toujours! (cf la citation de Landau, l'état est toujours solution des équations,

mais il est inobservable...)

Lorsque le paramètre w/w₀traverse la valeur unité le système bifurque.
Le concept de stabilité est plus général. Soit un état donné (équilibre, périodique, non régulier) On le

perturbe, que se passe-t-il et pour quel type de perturbation?

4. Calculs numériques:

On résoutpar une méthode de Runge Kutta à l'ordre 4, une technique classique et facile à mettre en
oeuvre - ce qui explique son succès pour les équations différentielles ordinaires avec conditions

initiales-. On pose q(t)=u(t) et u'(t)=up(t), et on réécrit le système
q
¨_{+ a q}^._{+ w02 sinq-w2sinqcosq = 0,}

sous la forme d'un système du premier ordre en temps:

u' = up

up' =
-aup - w₀² sin u-w²(sin u) (cos u).

6

5 Décembre 1997introduction