Droplets and bubbles animation and image gallery
Drops and
Bubbles page Collaborators
Legacy (historic) simulations
Atomization simulations
Two-dimensional atomizing jets, gas and liquid jets
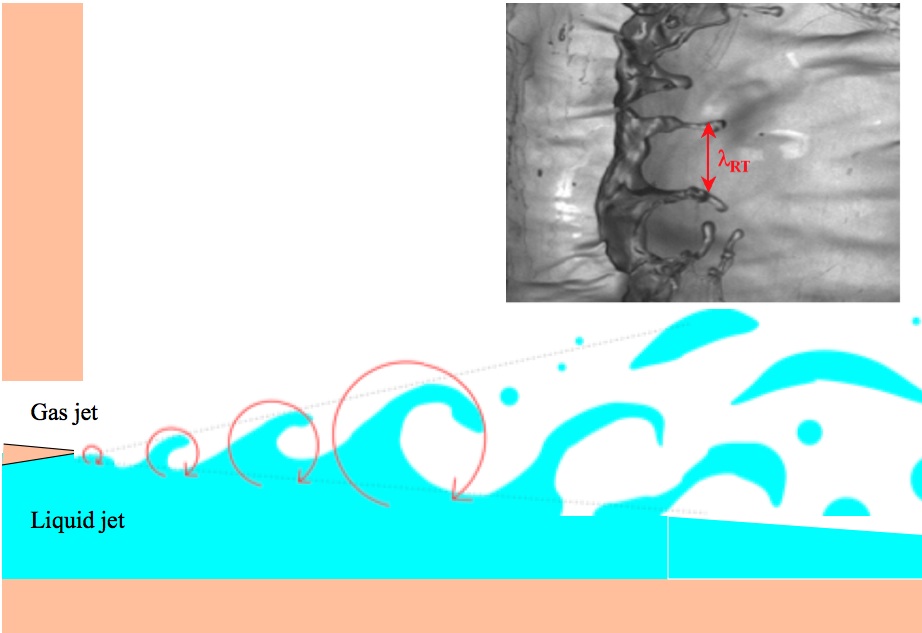 Schematics of the
Grenoble atomization experiment. (Emil Hopfinger, Ludovic Raynal, Alain Cartellier and others).
Two superposed planar jets realize an approximately 2D air-water mixing layer.
The inset shows a view of the Kelvin-Helmholtz waves from the top. The spacing between the fingers, that is the
transverse wavelength of the instability is
labelled "lambda_RT" in reference to the Rayleigh-Taylor theory of Hopfinger and Cartellier. The longitudinal and transverse
wavelengths of the instability are key ingredients in predicting the droplet size. Various theories are in competion to
predict these wavelengths in a wide range of velocity, density and viscosity ratios as well as in a range of Reynolds
and Weber numbers. The two-dimensional simulations shown next are perfomred in order to better understand the
formation of the longitudinal structures and wavelengths.
Schematics of the
Grenoble atomization experiment. (Emil Hopfinger, Ludovic Raynal, Alain Cartellier and others).
Two superposed planar jets realize an approximately 2D air-water mixing layer.
The inset shows a view of the Kelvin-Helmholtz waves from the top. The spacing between the fingers, that is the
transverse wavelength of the instability is
labelled "lambda_RT" in reference to the Rayleigh-Taylor theory of Hopfinger and Cartellier. The longitudinal and transverse
wavelengths of the instability are key ingredients in predicting the droplet size. Various theories are in competion to
predict these wavelengths in a wide range of velocity, density and viscosity ratios as well as in a range of Reynolds
and Weber numbers. The two-dimensional simulations shown next are perfomred in order to better understand the
formation of the longitudinal structures and wavelengths.
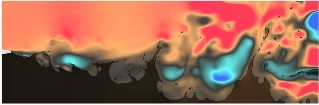 Atomization of a 2D air-water mixing layer
(128 Mbytes, Daniel Fuster and Jérôme Hoepffner)
Atomization of a 2D air-water mixing layer
(128 Mbytes, Daniel Fuster and Jérôme Hoepffner)
In this simulation a planar liquid layer is flowing under a faster gas layer. The simulation is described
in detail in Agbaglah et al. (2010), see references.
The simulation was performed using Gerris.
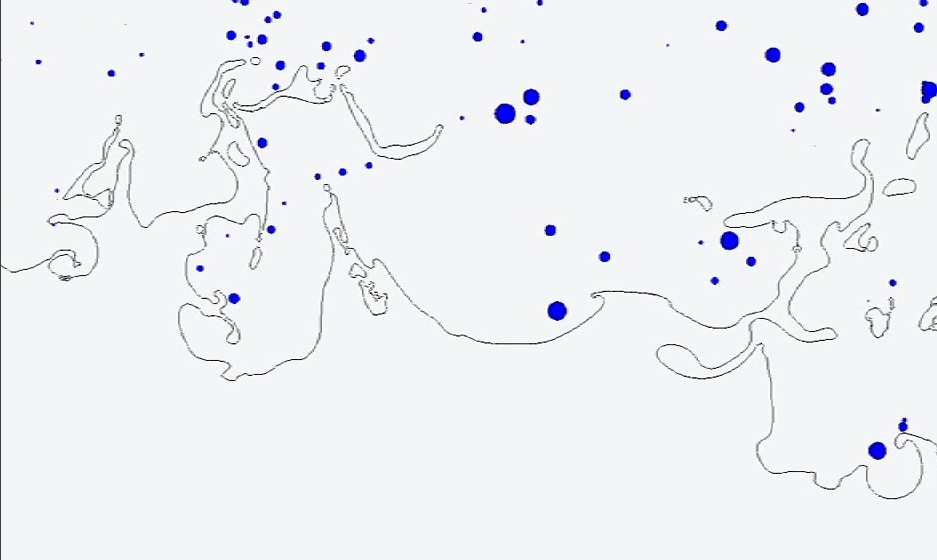 Lagrangian Particle Atomization Simulation (5 Mbytes, click on image to view movie). (Gaurav Tomar, Daniel Fuster, Stephane Popinet and Stephane Zaleski). In this simulation, small patches of fluid (two-dimensional "droplets" or rather cylinders) are transformed
into Lagrangian particles. Lagrangian particles follow a trajectory determined by the modelled particle forces (such as drag, lift and gravity, as well as several others). When a Lagragian particle collides with a large patch of liquid, its mass is transferred again to the "resolved" description. The resolved description uses the VOF tracking scheme. Details of the scheme are given in Tomar et al. (2010).
Lagrangian Particle Atomization Simulation (5 Mbytes, click on image to view movie). (Gaurav Tomar, Daniel Fuster, Stephane Popinet and Stephane Zaleski). In this simulation, small patches of fluid (two-dimensional "droplets" or rather cylinders) are transformed
into Lagrangian particles. Lagrangian particles follow a trajectory determined by the modelled particle forces (such as drag, lift and gravity, as well as several others). When a Lagragian particle collides with a large patch of liquid, its mass is transferred again to the "resolved" description. The resolved description uses the VOF tracking scheme. Details of the scheme are given in Tomar et al. (2010).
Three-dimensional atomizing liquid jet
 Atomization of a 3D jet
(13 Mbytes, Stéphane Popinet, Anne Bagué, Shricharan Yarlagadda and Stéphane Zaleski using the
Gerris code. This simulation reproduces closely the conditions in an automotive engine,
however the liquid jet is pulsed to trigger the instability in a more spectacular manner (Untriggered jets tend to have boring
behavior, see legacy simulations.
The Diesel fuel jet has a diameter under a millimeter
and a velocity over 100 meters/second. The Reynolds number is 5800. Air pressure is high at the relevant phase of the engine cycle
so the air to liquid density ratio is about 30. Oct-tree adaptive mesh refinement allows to have a resolution equivalent, in the
the finest grid regions, to that of a simulation with 16 billion grid points.
A similar simulation
can be reproduced following the Gerris example.
Atomization of a 3D jet
(13 Mbytes, Stéphane Popinet, Anne Bagué, Shricharan Yarlagadda and Stéphane Zaleski using the
Gerris code. This simulation reproduces closely the conditions in an automotive engine,
however the liquid jet is pulsed to trigger the instability in a more spectacular manner (Untriggered jets tend to have boring
behavior, see legacy simulations.
The Diesel fuel jet has a diameter under a millimeter
and a velocity over 100 meters/second. The Reynolds number is 5800. Air pressure is high at the relevant phase of the engine cycle
so the air to liquid density ratio is about 30. Oct-tree adaptive mesh refinement allows to have a resolution equivalent, in the
the finest grid regions, to that of a simulation with 16 billion grid points.
A similar simulation
can be reproduced following the Gerris example.
Droplet impact and jet breakup
 Gerris simulation of a splash performed by Pascal Ray using the
Gerris code.
(8 Mbytes). This simulation shows the early stages of the impact of a droplet on a layer of the same liquid.
At sufficiently large velocities and small viscosities, the impact generates a corolla or ejecta sheet that immediately
branches into fingers and droplets. Initial spacing of the fingers and droplets is small and grows in time
with a scaling comparable to that of the Plateau-Savart-Rayleigh instability.
Gerris simulation of a splash performed by Pascal Ray using the
Gerris code.
(8 Mbytes). This simulation shows the early stages of the impact of a droplet on a layer of the same liquid.
At sufficiently large velocities and small viscosities, the impact generates a corolla or ejecta sheet that immediately
branches into fingers and droplets. Initial spacing of the fingers and droplets is small and grows in time
with a scaling comparable to that of the Plateau-Savart-Rayleigh instability.
Bubble dynamics
 Bubble bursting
at a free surface. This movie was produced by Laurent Duchemin with Stéphane
Popinet's 2D axisymmetric front-tracking (marker chain)
code.
Bubble bursting
at a free surface. This movie was produced by Laurent Duchemin with Stéphane
Popinet's 2D axisymmetric front-tracking (marker chain)
code.
 Bubble
bursting at a free surface, cut view with vorticity.
Bubble
bursting at a free surface, cut view with vorticity.
 Schematics of the
Grenoble atomization experiment. (Emil Hopfinger, Ludovic Raynal, Alain Cartellier and others).
Two superposed planar jets realize an approximately 2D air-water mixing layer.
The inset shows a view of the Kelvin-Helmholtz waves from the top. The spacing between the fingers, that is the
transverse wavelength of the instability is
labelled "lambda_RT" in reference to the Rayleigh-Taylor theory of Hopfinger and Cartellier. The longitudinal and transverse
wavelengths of the instability are key ingredients in predicting the droplet size. Various theories are in competion to
predict these wavelengths in a wide range of velocity, density and viscosity ratios as well as in a range of Reynolds
and Weber numbers. The two-dimensional simulations shown next are perfomred in order to better understand the
formation of the longitudinal structures and wavelengths.
Schematics of the
Grenoble atomization experiment. (Emil Hopfinger, Ludovic Raynal, Alain Cartellier and others).
Two superposed planar jets realize an approximately 2D air-water mixing layer.
The inset shows a view of the Kelvin-Helmholtz waves from the top. The spacing between the fingers, that is the
transverse wavelength of the instability is
labelled "lambda_RT" in reference to the Rayleigh-Taylor theory of Hopfinger and Cartellier. The longitudinal and transverse
wavelengths of the instability are key ingredients in predicting the droplet size. Various theories are in competion to
predict these wavelengths in a wide range of velocity, density and viscosity ratios as well as in a range of Reynolds
and Weber numbers. The two-dimensional simulations shown next are perfomred in order to better understand the
formation of the longitudinal structures and wavelengths.
 Atomization of a 2D air-water mixing layer
Atomization of a 2D air-water mixing layer Lagrangian Particle Atomization Simulation (5 Mbytes, click on image to view movie)
Lagrangian Particle Atomization Simulation (5 Mbytes, click on image to view movie) Atomization of a 3D jet
Atomization of a 3D jet Gerris
Gerris Bubble bursting
at a free surface. This movie was produced by Laurent Duchemin with Stéphane
Popinet's 2D axisymmetric front-tracking (marker chain)
code.
Bubble bursting
at a free surface. This movie was produced by Laurent Duchemin with Stéphane
Popinet's 2D axisymmetric front-tracking (marker chain)
code.
 Bubble
bursting at a free surface, cut view with vorticity.
Bubble
bursting at a free surface, cut view with vorticity.