Nous nous somme attachés à vérifier numériquement les lois de puissances obtenues par Bickley pour la vitesse sur l’axe central du jet et son enveloppe.
La solution de Bickley prévoit une décroissance de la vitesse sur l’axe central en puissance –1/3 de l’altitude (x).
Nous traçons cette vitesse pour un nombre de pas de temps suffisamment grand pour qu’un état stationnaire soit atteint, en pratique de l’ordre de 5000 itérations. (Figures II.2 et II.3).
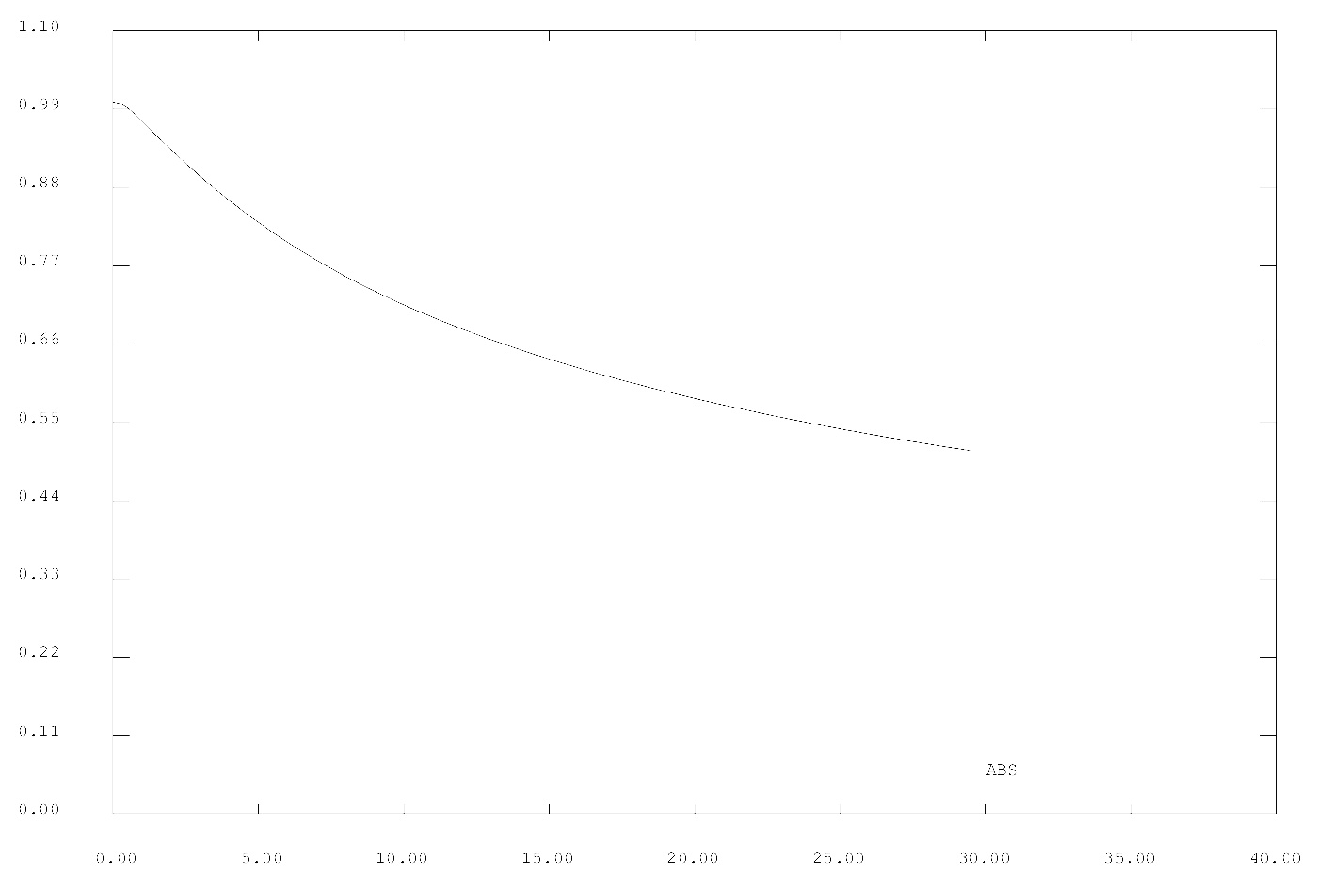
- Figure II.2 : Vitesses sur l'axe d'un jet stationnaire pour Re=50 fournies par Castem -
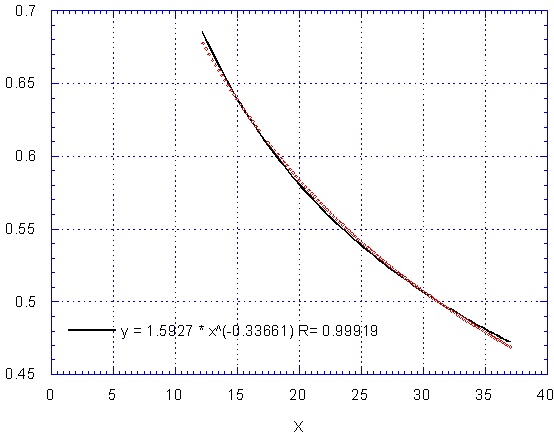
- Figure II.3 : Régression en puissance sur l'intervalle [12,38] -
La loi de puissance en –1/3 est vérifiée de façon très satisfaisante à partir d’une altitude de l’ordre de 4 à 5 largeurs de la cheminée, d'autant plus qu'on se place à nombre de Reynolds faible (un grand nombre de Reynolds provoque l'instabilité de la solution calculée, et on ne peut donc pas suivre les hypothèses des calculs analytiques précédents). Avant, l’écart aux prévisions s’explique facilement : Bickley suppose une vitesse d’introduction infinie par un orifice ponctuel, donc la loi en diverge logiquement en s’approchant du sol. Au contraire, dans notre modélisation, la vitesse initiale est finie et la largeur de la cheminée non nulle donc notre solution quitte celle de Bickley pour se raccorder au Poiseuille de sortie lorsque x tend vers 0.
D’après la solution de Bickley, le paramètre
d’auto-similitude h étant
constant sur les courbes d’équation y = A x2/3,
on s’attend à ce que la largeur du jet suive une loi en
puissance 2/3.
- Figure II.4 : Champ des vitesses en x = 0, 4, 8, 12, 16 et 19 -
En traçant le lieu des point tels que U=Umax/2 ou Umax/4 (où, à x fixé, Umax est la vitesse sur l’axe), on observe que ces courbes, qui constituent les enveloppes du jet, suivent approximativement une loi en puissance 2/3. (Figure II.5)

- Figure II.5 : Régressions pour Umax/2 et Umax/4-
Pour ces deux vérifications, il faut rappeler que l'on se place dans un cadre assez éloigné de la théorie: Le nombre de Reynolds n'est pas très élevé et l'orifice d'entrée n'est pas ponctuel.