pyl(a)ccr.jussieu.fr
http://www.lmm.jussieu.fr/~lagree/SIEF/GRAVITATION/RDV/rdv.html
créé 11/2006 aj 02/11/2018
Les Rendez Vous Spatiaux vus
par PYL, c'est
spécial!!!
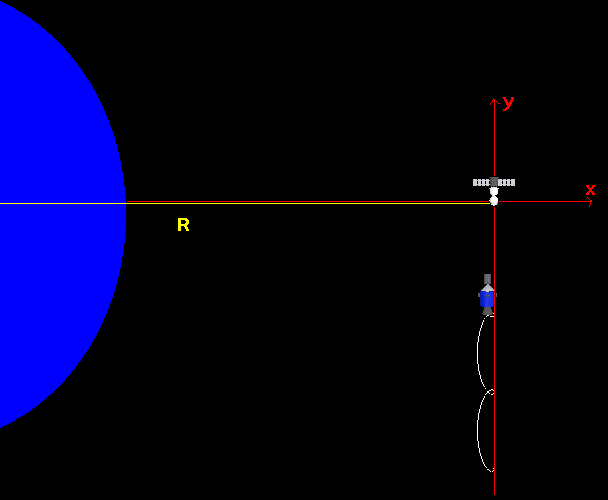 |
On travaille dans le plan de la trajectoire de la cible
(on oublie z, que l'on peut rajouter sans peine car
l'équation est découplée).
Le vaisseau cible ("S" comme Soyouz) tourne autour de la terre sur une
orbite circulaire, on écrit que son
accélération est égale à la
force de graviation de Newton.
Dans le repère lié à la cible, la
position du vaisseau chasseur ("A" comme Apollo) est
x et y.
L'accélération ressentie dans ce
repère relatif est donc l'accélération
précédente plus la partie Coriolis, plus la
partie liée à la rotation du
référentiel.
La force subie par le vaisseau A est la force de Newton
estimée au point A.
La développement entre la force en S et en A qui est
très proche (par rapport au centre de la terre) donne des
termes linéaires dans les équations.
|
Lorsque l'on met tout cela en équations on obtient au bout
du compte les équations de Hill
CLOHESSY-WILTSHIRE
En fait, les équations de Hill seraient issues du système précédent en
ajoutant en plus la force d'attraction de la cible, en supposant
qu'elle est faible mais pas nulle et en supposant que la distance
Terre-cible (donc ici Terre-Lune) grande. Les équations sont appropriées pour
calculer les trajectoires d'un vaisseau autour de la Lune. lorsque l'on
fait tendre vers 0 la masse de la cible, on obtient les équations de
Clohessy-Wiltshire.
La position et la vitesse relative r = xex + yey et vr = x′ex + y′ey
La vitesse absolue est la somme de la vitesse
d’entraînement et de la vitesse relative :
va = ve + vr
L’accélération absolue γa est la somme de
l’accélération
d’entraînement, de
l’accélération relative et de
l’accélération de Coriolis
γa = γe + γr + γc
avec γc = 2ω × r et γr = x′′ex + y′′ey
La vitesse et l’accélération
d’entraînement sont celles d’un mouvement
circulaire,
soit : ve = ω × r
L’accélération
d’entraînement est exactement
l’accélération du vaisseau cible.
C’est
donc la valeur de la force de Newton :
γe = -GM∕(R2)ex et on a ω2 = (GM∕R3)
or l’accélération
d’entraînement est par définition
γe = dω∕dt
× r + ω
× ve avec ω = (GM∕R3)1∕2 constante.
tandis que l’accélération de Coriolis
est :
γc = 2(-ωy′ex + ωx′ey) et ω × (ω × r) = -ω2xex - ω2yey
Mais,
l’accélération absolue est la force de
Newton appliquée sur le vaisseau
chasseur :
γa = -GM((R + x)ex + yey)∕∣((R + x)ex + yey)∣3
On obtient donc le
développement de :
γa - γe = GM(Rex∕R3 - ((R
+ x)ex + yey)∕∣((R + x)ex + yey)∣3 or
((R +
x)ex + yey)∕∣((R + x)ex + yey)∣3 =
= (1∕R2)(1 + (x∕R)ex + (y∕R)ey)(1 - (3∕2)(2x∕R) + ...)
ce qui nous donne :
γa - γe = -(GM∕R3)((1 - 3)xex + yey) + ... = -ω2(-2xex + yey) + ...
On a ainsi
l’accélération relative :
x′′ex + y′′ey = -(ω2(-2xex + yey) + ...) -
2(-ωy′ex + ωx′ey) + ω2xex + ω2yey
d’où les
équations finales à résoudre :
x′′ = 2ωy′ + 3ω2x et y′ = -2ωx′
La solution
générale est obtenue en remarquant que
x′′′
= -4ωx′ + 3ω2x′
soit (x′)′′ = ω2(x′)
soit x = B1cos(ωt)
+ B2sin(ωt)
+ B3
Substitué dans la deuxième y = C1 + tC2 + 2B2cos(ωt)
- 2B1sin(ωt)
Puis, en écrivant que x(0) = x0,y(0) = 0,x′(0)
= u0,y′(0)
= v0, on obtient tout
simplement :
x(t) = (2v0∕ω + 4x0) - (2v0∕ω + 3x0)cos(ωt)
+ u0∕ωsin(ωt)
y(t) = (-2u0∕ω + y0) - (3v0 + 6ωx0)t + 2u0∕ωcos(ωt) + (4v0∕ω + 6x0)sin(ωt)
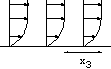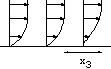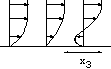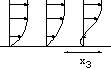
Quelques exemples, de gauche à droite (vus de
différentes hauteurs)
1) x0=y0=0,
u0=-1, v0=0
(on va sur la gauche, Coriolis fait tourner à droite,
l'orbite est un cercle),
2) x0=y0=0, u0=0, v0=1 (on va vers l'avant,
puis
on recule!)
3) x0=y0=0, u0=0 v0=-1 (on recule puis on va vers
l'avant)

Pour aller plus loin
A titre d'exercice (c.f. J. Kevorkian & J.D. Cole, Perturbation Methods in Applied Mathematics, Springer
(1981)), on pourra établir les vraies équations de Hill. Il s'agit donc du
mouvement d'un vaisseau près de la Lune (et perturbé par la Terre).
C'est
bien entendu une variante du fameux problème à "Trois Corps".
Si on appelle μ la masse réduite, on obtient les équations
adimensionnées suivantes pour
x et y:
x′′ = -μx/(x^2+y^2)^(3/2) + 2 y′
+3x
y′′ = -μy/(x^2+y^2)^(3/2) - 2 x′.
à l'échelle μ^(1/3) pour x et y
on a par moindre dégénérescence le système le
plus complet: les équations de Hill.
Si on reste à l'échelle 1, et que l'on fait tendre μ vers 0 on obtient
les équations de Clohessy -Wiltshire.
voir aussi l'annexe du
cours PYL sur l'asymptotique.