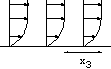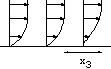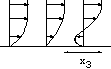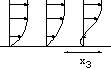
Départ impulsif d'un cylindre,
m à j 2003
Séparation instationnaire de la couche limite
La vitesse extérieure (de fluide parfait) est imposée elle
vaut:
U(x,t)=sin(x).
C'est la vitesse de fluide parfait autour d'un cylindre (superposition du
doublet et de l'écoulement uniforme).
Pour x tendant vers 0 on retrouve le point d'arrêt, pour
π/2 < x < π
l'écoulement est décelléré: il peut donc produire la séparation de la
couche limite...
Sur ces animations on observe la singularité en temps fini
associée à la séparation de la couche limite.
Elle apparaît
dans les équations de couche limite instationnaires à vitesse extérieure
imposée avec gradient défavorable (ce qui est le cas ici).
Il s'agit de la singularité de
Van Dommelen, L. L. & Shen, S. F. (1980)
"The spontaneous generation of the singularity in a
separating laminar boundary layer". Journal of Computational Physics 38 125-140.
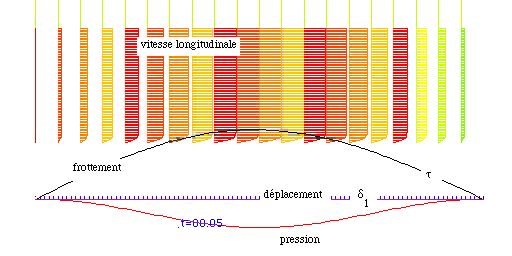
Séparation:
- évolution de l'épaisseur de couche limite
delta1
dans le cas du cylindre.
- Départ du tourbillon sur
un cylindre.
- Evolution de l'épaisseur de couche limite du frottement pariétal
et profils de vitesses.
On observe (film.mov) la formation de la singularité de la couche limite au
bout d'un temps (adim.) environ égal à 3...