| PYL créé 12/12 àj 2012 | Ecoulement de point
d'arrêt avec thermique Solution de Hiemenz ou point d'Arrêt par Gerris |
 |
| PYL créé 12/12 àj 2012 | Ecoulement de point
d'arrêt avec thermique Solution de Hiemenz ou point d'Arrêt par Gerris |
 |
| Photos de points d'arrêts extraites du livre de Milton Van Dyke, l'écoulement vient de la gauche et se divise entre l'intrados et l'extrados à cet endroi: |

| Solution de Fluide Parfait poiur le point d'arrêt: u=x, v=-y Cet écoulement est connu sous le nom de "écoulement de Hiemenz", il admet une solution autosemblable et c'est aussi une solution exacte des équations de Navier Stokes: u=xf'(y), v=-f(y).
l'épaisseur de couche limite est constante: δ = O(1/sqrt(Reynolds)) Solution de Hiemenz f'''(y)+f(y)f''(y)+(1-f'(y)f'(y))=0 f(0)=f'(0)=0 f()=1 g'''(y)+f(y)g'(y)=0 g(1)=1 g(0)=0 |
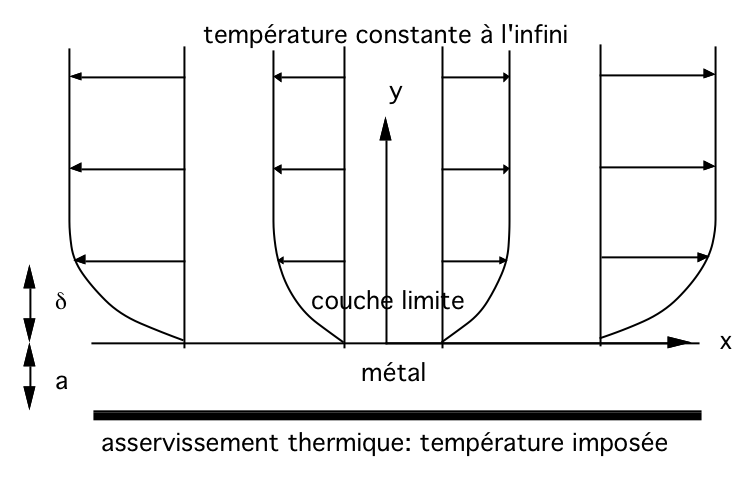 |
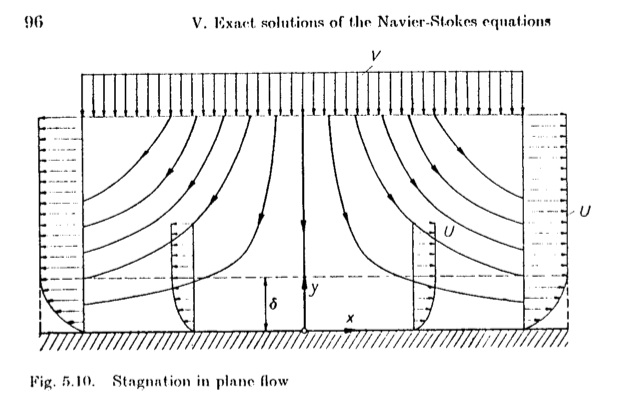 configuration du point d'arrêt, image de Schlichting Détails de la solution dans Schlichting |
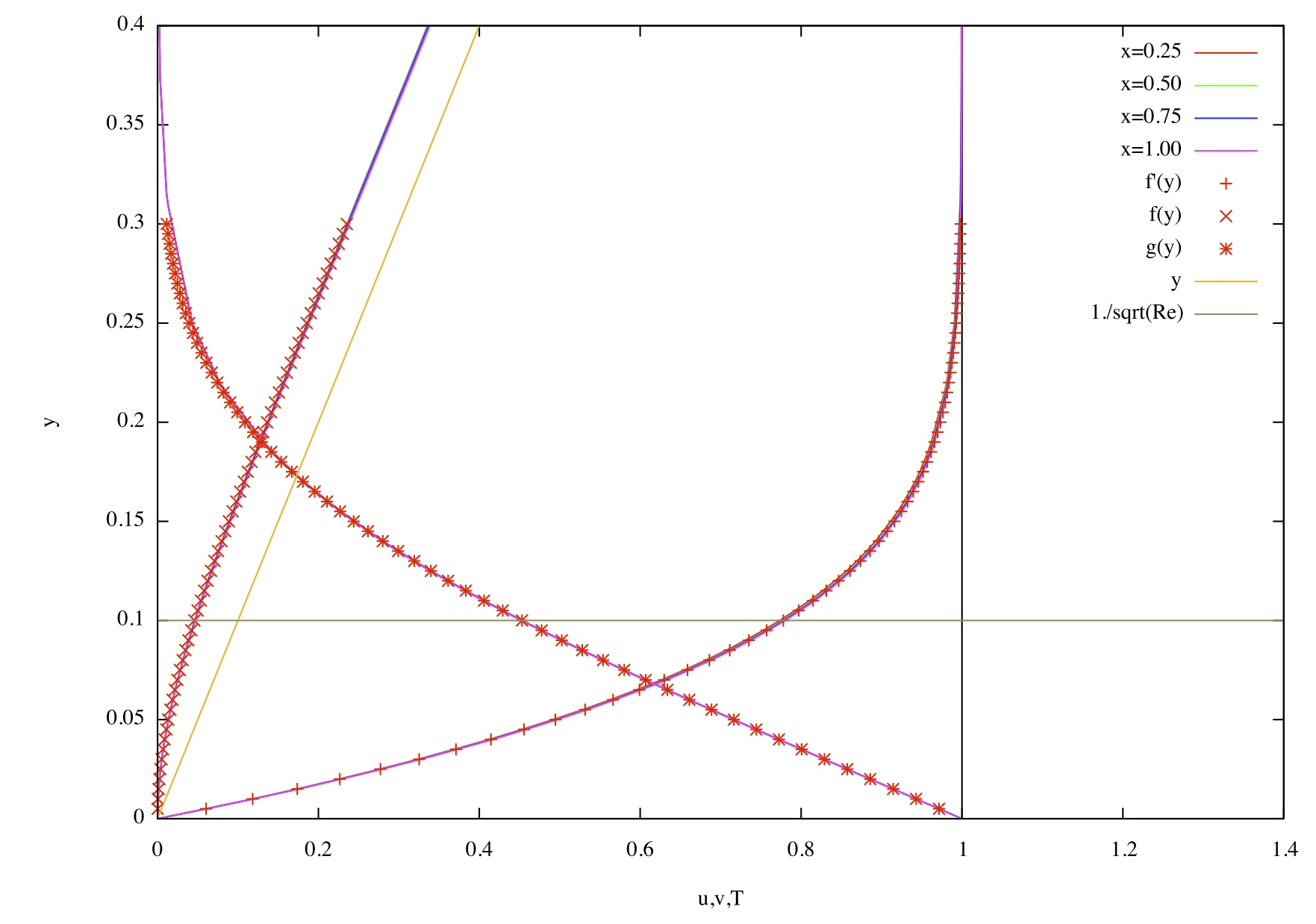 solution de Hiemenz et Calcul Gerris pour le cas Re=100 |
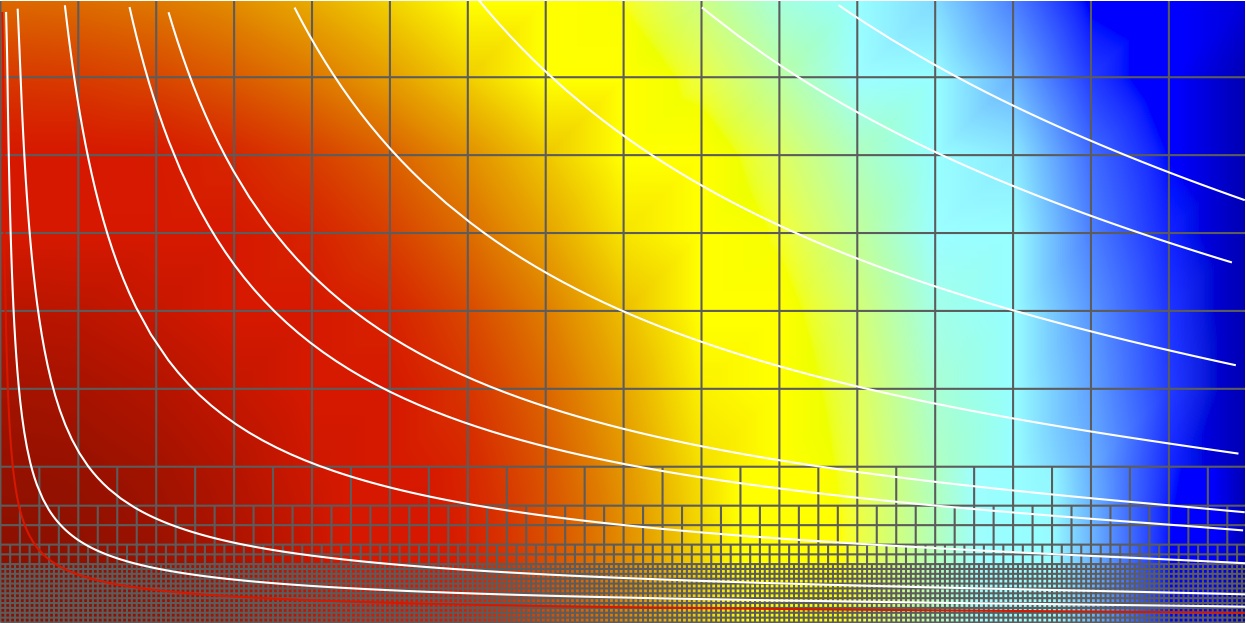 Pression et lignes de courant |
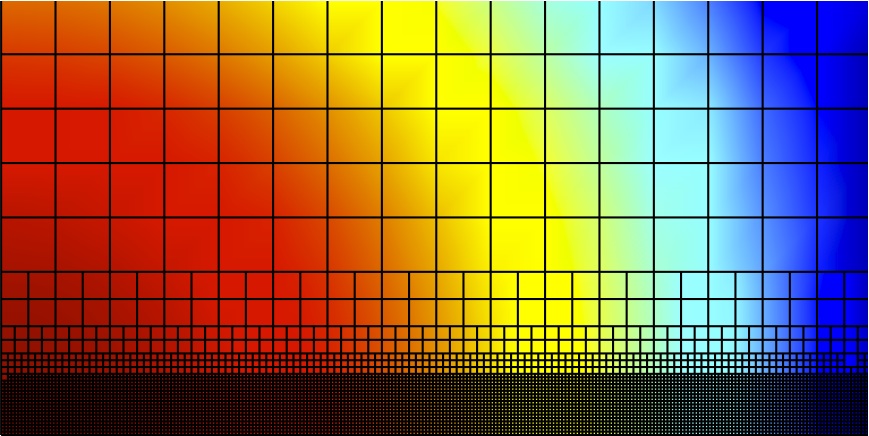 Pression |
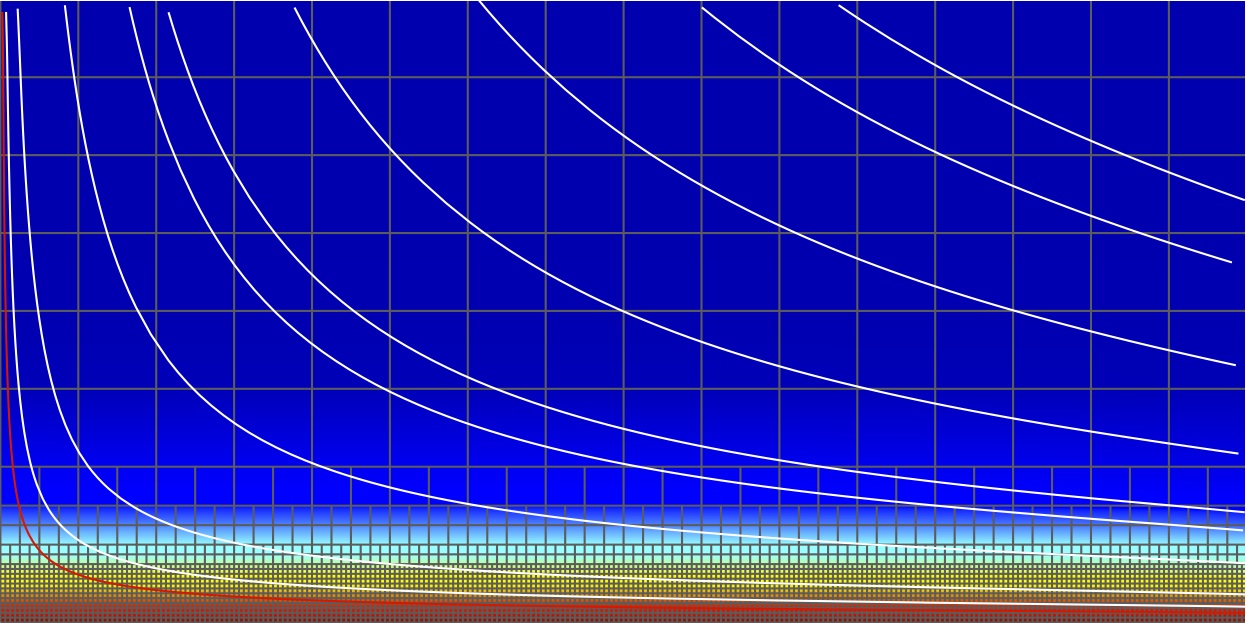 Température |