| PYL créé 02/07 àj 2012 | Ecoulement de point d'arrêt avec thermique |  |
| PYL créé 02/07 àj 2012 | Ecoulement de point d'arrêt avec thermique |  |
| Photos de points d'arrêts extraites du livre de Milton Van Dyke, l'écoulement vient de la gauche et se divise entre l'intrados et l'extrados à cet endroi: |

| Cet écoulement est connu sous le nom de
"écoulement de Hiemenz", il admet une solution autosemblable
et
c'est aussi une solution exacte des équations de
Navier
Stokes: u=xf'(y), v=-f(y).
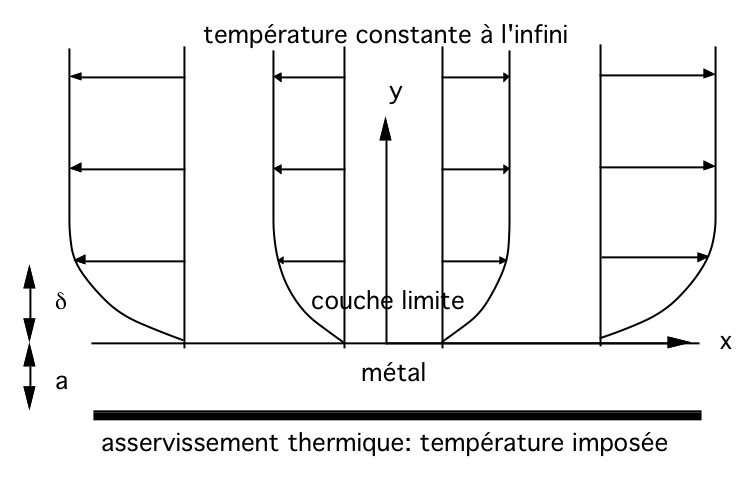
soit l'épaisseur "a" de la lamelle, ks la conductivité du solide, l'épaisseur de couche limite: δ = O(1/sqrt(Reynolds)) |
 |
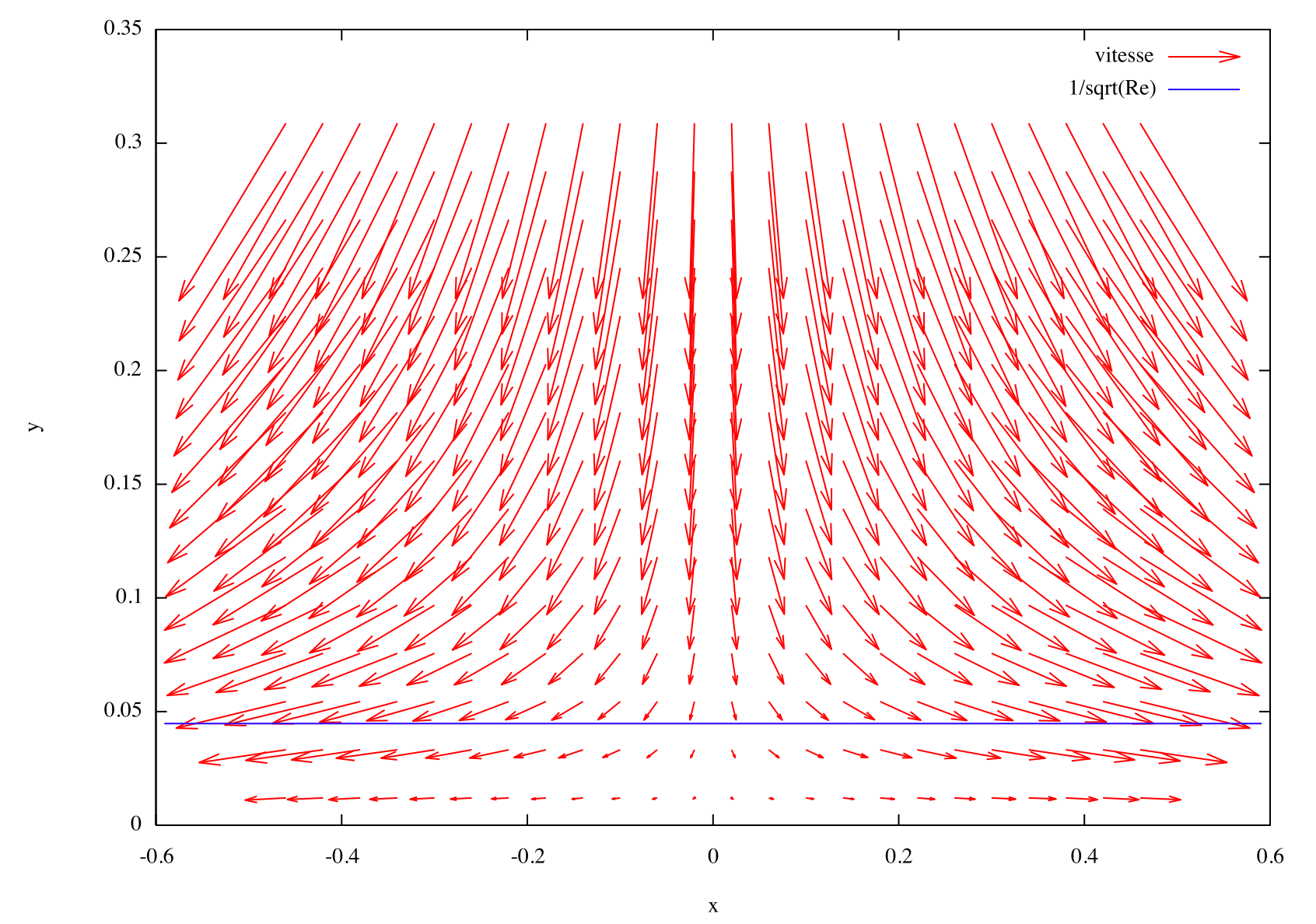 Champ de vitesse
(u,v) calculé par FreeFEMM++
|
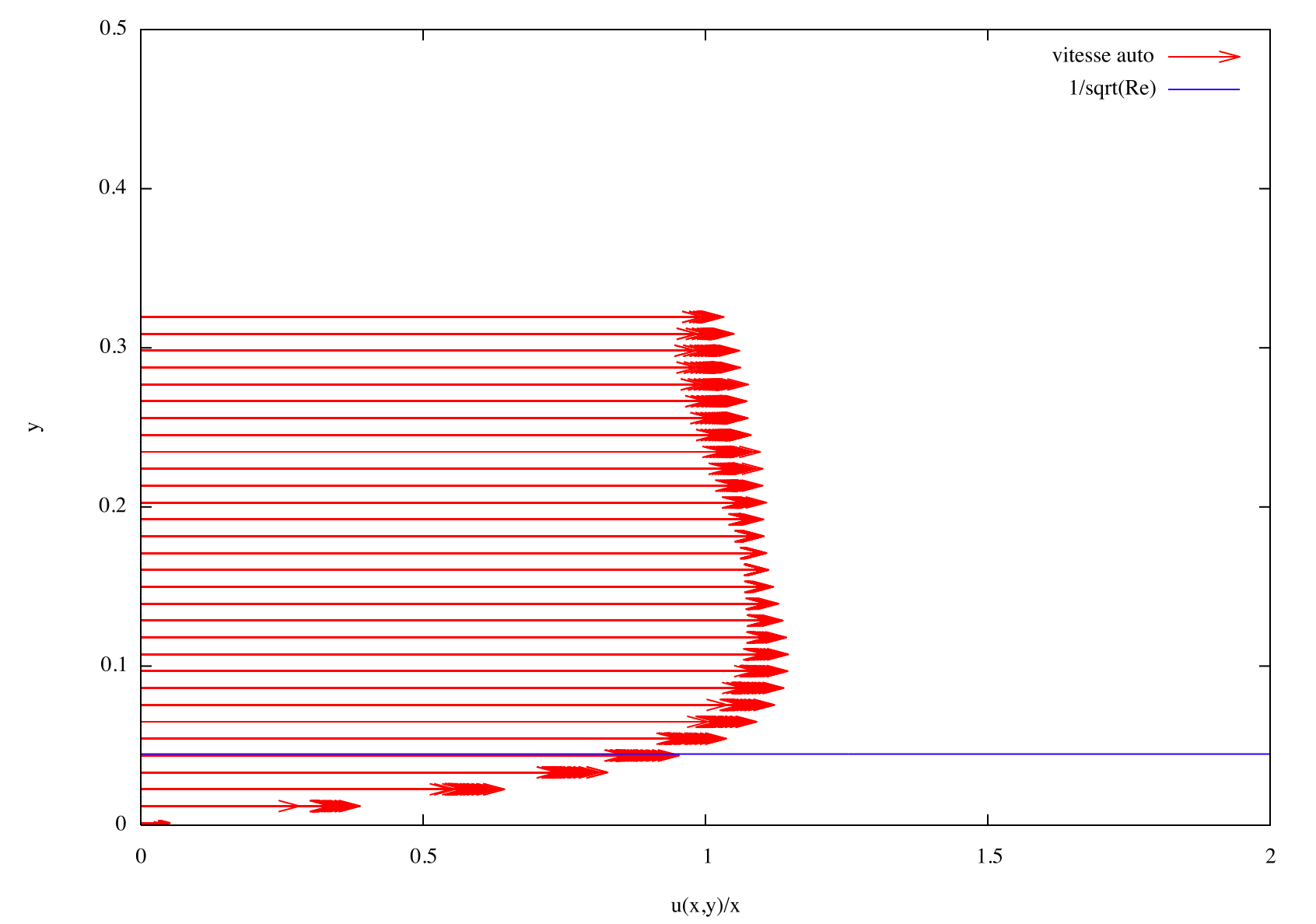 vérification
du
caractère autosemblable de la vitesse on trace le rapport de
u(x,y) par la distance au point d'arrêt x. La surcroissance
de
vitesse est un subtil effet de second ordre.
|
| Exemple de résolution instationnaire à Reynolds = 500; ks = 0.1 b=(e/ks/sqrt(Reynolds))
b= 0.0894427, petit nombre de Biot (point de vue du solide, en effet on voit sur le film que la température finale est à peut près constante dans le solide avec une Température de paroi Tp=0.9179. La température varie ensuite peu dans le fluide, on voit la couche limite). Pour les temps courts, on voit l'évolution temporelle (iso T) de la température dans la lamelle uniquement, puis au bout d'un certain temps le fluide est chauffé. |
 |
| On remarque que la température ne dépend pas de x, sur le dessin ci contre à stationnarisation, tous les profils de température se superposent bien. | 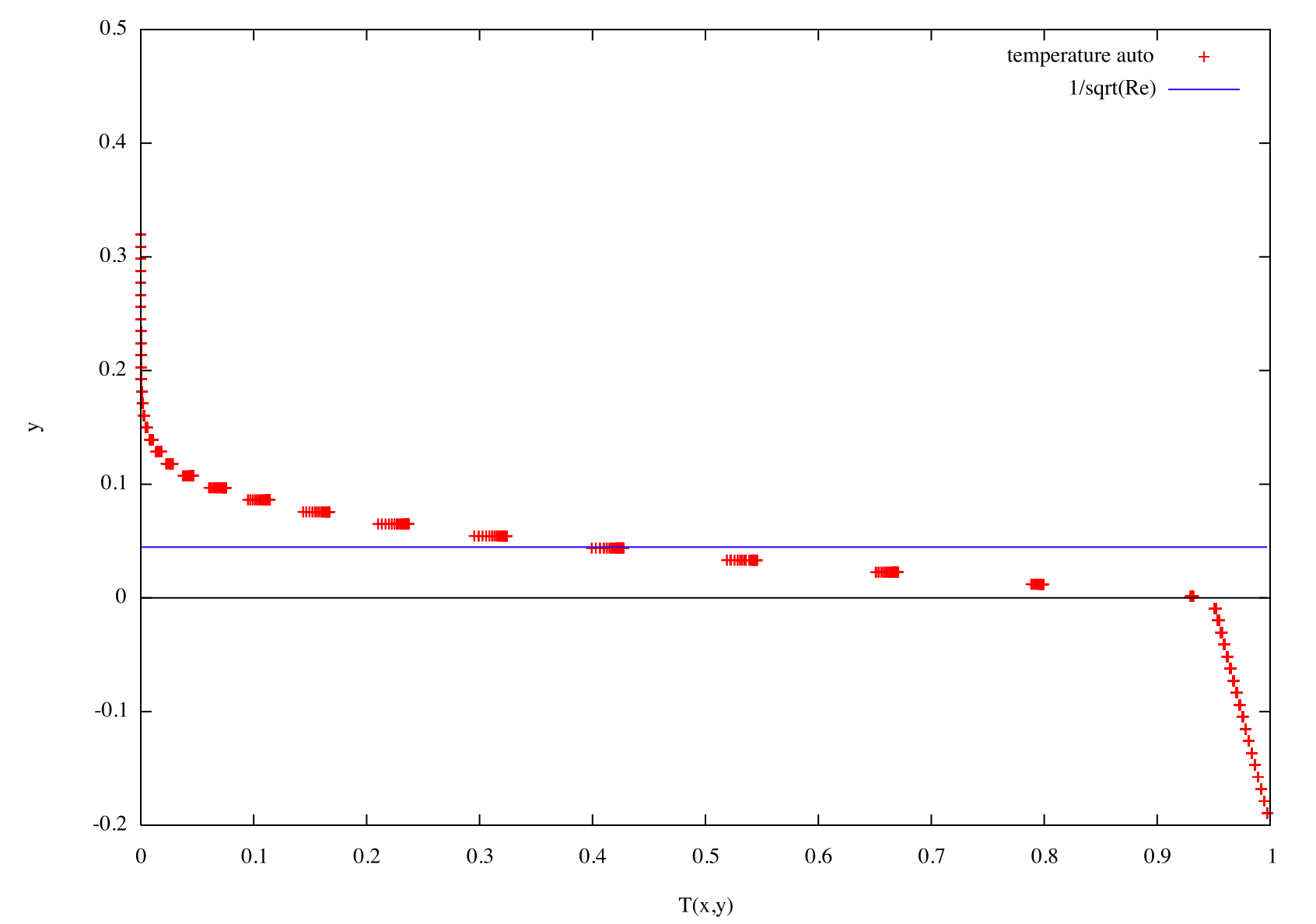 |
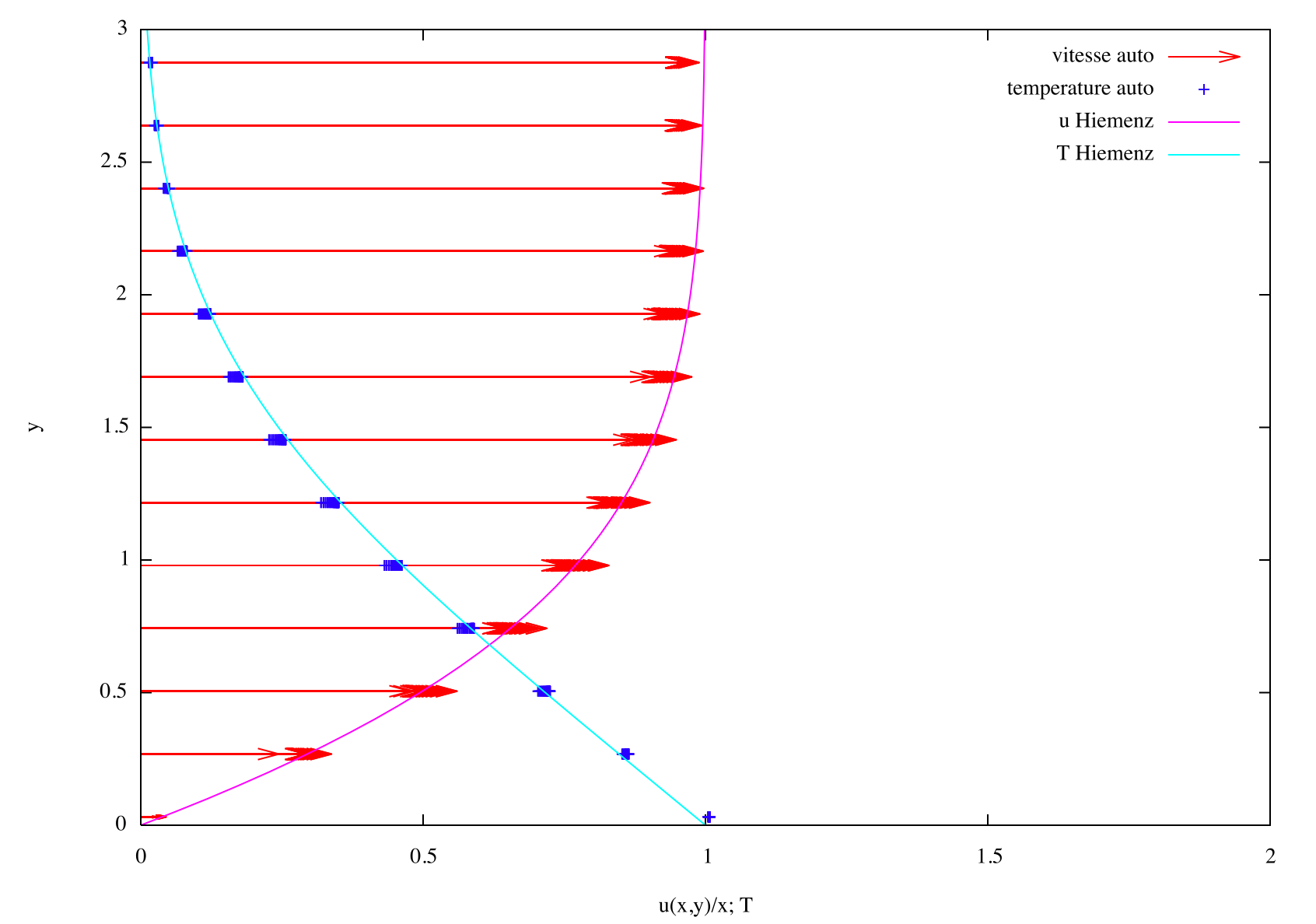
| On vérifie la superposition de la vitesse et
de la température autosemblable. f'''[y] + f[y]f''[y] + 1 - f'[y] f'[y] = 0 f''[0]=1.23 Pr = 1; g''[y] + Pr (f[y] g'[y]) =0; g'[0]=-0.57 |
 |
|
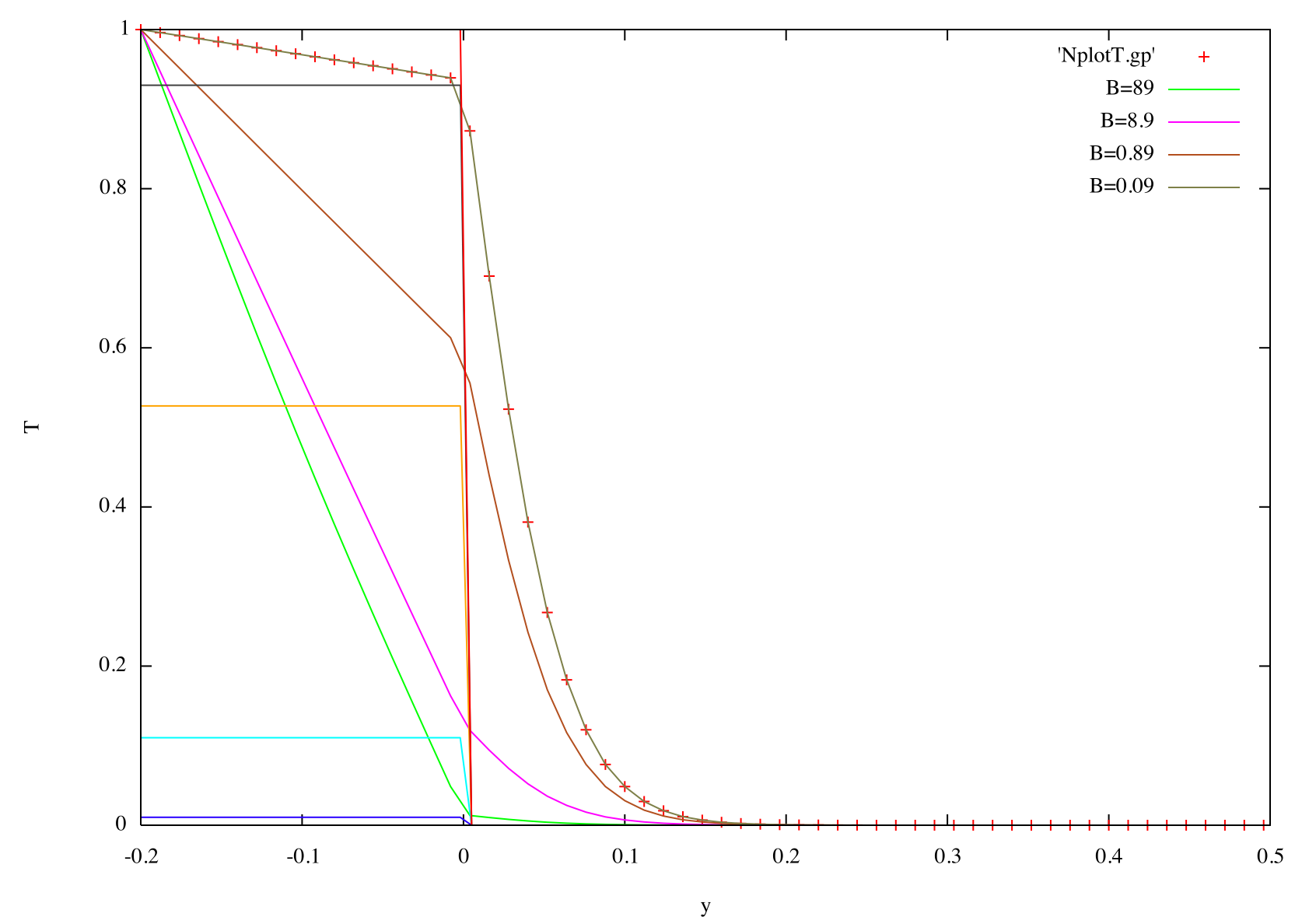
Exemples de
profils de
températures finales perpendiculairement au point
d'arrêt.
La température finale est bien linéaire dans la
lamelle,
et décroît dans la couche limite du fluide.
Pour un grand nombre de Biot (relatif au solide défini par (e/ks/sqrt(Reynolds))), la température varie fortement dans la lamelle. Pour un petit nombre de Biot (relatif au fluide), la température varie peu dans la lamelle. Et inversement pour le fluide. |
 |