Drops and bubbles: deformation, break-up, atomization
Coworkers Contacts
Animations
The breaking of a powerful ocean wave in gigantic sprays,
the myriad droplets ejected by a flying liquid drop when it impacts and splashes
on an obstacle, the delicate flutter of microscopic droplets emitted by a
bubble bursting on a free liquid surface
are fascinating events. The numerical simulation of such droplets, bubbles and waves
is the focal point of the research reported in these pages. These numerical simulations
are a fairly complex problem of applied mathematics and computational mechanics. They require
the research, development and coding of specific methods for free surfaces and
fluid interfaces.
Many researchers of d'Alembert working as a team have contributed to the development of
this methodology.
The numerical treatment of evolving interfaces, or surface tracking that we chose to perform
using principally volume-of-fluid (VOF) methods is now a maturing subject, with however many
theoretical and coding improvements still to come.
Computational calculations allow, under certain conditions,
a fair reproduction of the reality, so
called numerical experiments can be performed, useful both for
curiosity-driven and application-driven science.
Summary
In what follows we dwell on the following topics
 Atomization processes involve the development of the instabilities at the interface of
a high-speed jet. The combustion of liquid fuels requires their initial breakup into small droplets. Combustion technology thus provides a powerful incentive to study atomization. Injection devices present in both
petrol and diesel car engines control the atomisation of fuels and thus
the typical droplet size. This eventually
determines the quality of the combustion,
such as engine efficiency or pollution rate. We have
performed numerous calculations
of atomization.
Atomization processes involve the development of the instabilities at the interface of
a high-speed jet. The combustion of liquid fuels requires their initial breakup into small droplets. Combustion technology thus provides a powerful incentive to study atomization. Injection devices present in both
petrol and diesel car engines control the atomisation of fuels and thus
the typical droplet size. This eventually
determines the quality of the combustion,
such as engine efficiency or pollution rate. We have
performed numerous calculations
of atomization.
 Droplet
impacts on solid or liquid surface have become a cultural icon. It is also an important issue in engineering.
In agriculture, the penetration of rainwater depends strongly
upon the humidity of the soil. Impact of aerosol drops,
containing agricultural treatment products
is also of considerable interest as well. In internal combustion engines, the rebound on combustion chamber or pipe walls modifies the size of the droplets and
affects the combustion processes.
Droplet
impacts on solid or liquid surface have become a cultural icon. It is also an important issue in engineering.
In agriculture, the penetration of rainwater depends strongly
upon the humidity of the soil. Impact of aerosol drops,
containing agricultural treatment products
is also of considerable interest as well. In internal combustion engines, the rebound on combustion chamber or pipe walls modifies the size of the droplets and
affects the combustion processes.
 Bubble
dynamics and other topics: Bubble dynamics has extremely varied applications, in power plant technology, chemical engineering, biology and oceanography. A striking observation
is sonoluminescence:
when excited by strong acoustic waves, bubbles emit a brief light flash, visible
to the naked eye. Bubble
oscillations relate to several other important problems: the stability of
oscillating
bubbles, or jet formation
in a cavity for instance. Bubble dynamics is important in other engineering issues such
as the damage brought to hydraulic circuits or turbine vanes by cavitation.
Bubble
dynamics and other topics: Bubble dynamics has extremely varied applications, in power plant technology, chemical engineering, biology and oceanography. A striking observation
is sonoluminescence:
when excited by strong acoustic waves, bubbles emit a brief light flash, visible
to the naked eye. Bubble
oscillations relate to several other important problems: the stability of
oscillating
bubbles, or jet formation
in a cavity for instance. Bubble dynamics is important in other engineering issues such
as the damage brought to hydraulic circuits or turbine vanes by cavitation.
 Numerical methods: we have
developped numerical methods based on the idea of volume-of-fluid
interface tracking and height functions. Volume-of-fluid is a method
of interface tracking somewhat similar to level-sets, it provides
explicit tracking of the interface which is robust with respect to
topology changes and conserves mass to high accuracy and in some cases
to machine accuracy. It has been combined with height-function methods
and octree mesh refinement in the Gerris
code.
Numerical methods: we have
developped numerical methods based on the idea of volume-of-fluid
interface tracking and height functions. Volume-of-fluid is a method
of interface tracking somewhat similar to level-sets, it provides
explicit tracking of the interface which is robust with respect to
topology changes and conserves mass to high accuracy and in some cases
to machine accuracy. It has been combined with height-function methods
and octree mesh refinement in the Gerris
code.

Atomization
Gerris simulation of Diesel Jet. Click on image to enlarge
We have studied both the two and three-dimensional
instabilities of a liquid-gas interface in a shear flow. These instabilities
account in particular for liquid jet atomisation near the injection pipe.
They are therefore fundamental in the determination of processes for liquid
combustion.
Linear stability theory of small perturbations
for a parallel two-phase flow (Orr-Sommerfeld theory in variable density
case) is the first step in a systematic study of the instability. This theory is
unfortunately impossible to formulate analytically and numerical simulations
of the Orr-Sommerfeld equations are needed. P. Yecko and T. Boeck have shown the existence
of new unstable modes in the dynamics, unknown in the literature (Yecko, Zaleski & Fullana 2002, Boeck & Zaleski 2005, Boeck et al 2007, Bague et al. 2010, see references on atomization.
Transient three-dimensional growth was investigated by Yecko & Zaleski (2005).
Beyond linear instability growth, experiments
and numerical simulations are particularly revealing of the structures and mechanisms of atomization. For instance, sheet and fiber-like objects are universally observed at sufficiently high jet speed
(Lasheras or Hopfinger, Raynal and Villermaux).
This work also applied to
the study of atomisation in Diesel engine jets. In this context, we
have used adaptave mesh refinement on an oct tree, using the gerris code,
resulting in the image above.

Droplet impact and splashing
Gerris simulation of a splash performed by Pascal Ray. Click on image to enlarge
We have studied
both the fully three-dimensional and axisymmetric impacts of a droplet
on a solid surface,
see references on droplet impact
and splashing. Droplet impacts and collisions are found in all
areas of science and engineering. For instance in the droplet model of
atomic nuclei, collisions between nucleons may be modelled as droplets
collisions. Droplet impacts on the wall of combustion chambers play an
important role in determining the eventual size of the
droplets. Impact of agricultural sprays and rain droplet on soil and
plants is also noteworthy.
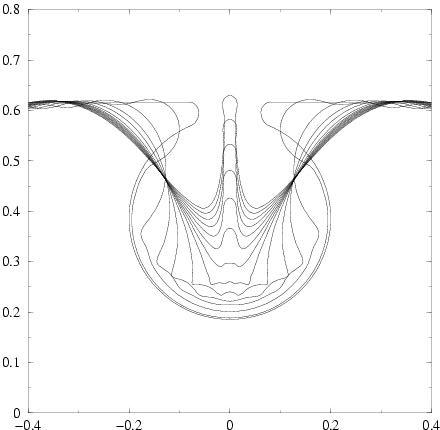
Axisymmetric simulation of droplet impact on a solid surface (Stéphane Popinet, Zhen Jian, Jie Li et Guy-Jean Michon)
The theory of axisymmetric droplet impact is rather difficult, despite some remarkable
advances of 2D potential flow theory. The actual impact involve viscous flow and potential
theory cannot apply except as an approximation in some regions of the flow. Surface tension
is also involved in an important way. Finally, compressible and molecular scale effect are probably important in the thin air layer below the impacting droplet.

Bubble dynamics and other topics
Front tracking simulation of a bubble bursting at a free surface performed by
Laurent Duchemin. Click on image to enlarge
Bubbles bursting at a free surface offer
fascinating dynamics, and play a rôle in cloud forming as well as in the
taste of champagne.
Oscillating bubbles in a liquid bulk present
complex dynamics such as sonoluminescence. (For our work on the subject
see references on bubble dynamics.)
An important point for understanding
the mechanism controlling sonoluminescence is that bubbles cannot
remain spherical.
The calculation of the deformation of oscillating bubbles
is a well-posed example of a free surface problem.
A systematic approach allowed to find the
role of the viscosity in the formation of the liquid jet observed in a
cavitation bubble near a wall.

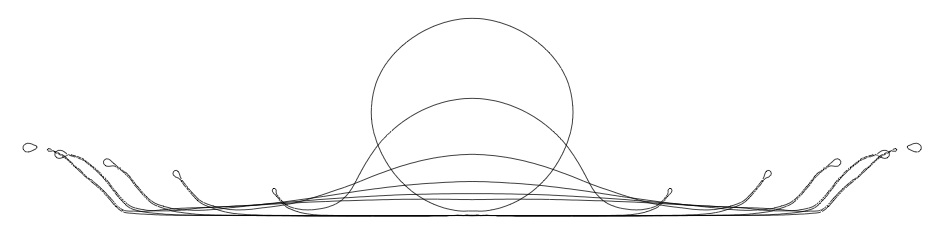
Central jet formed after a bubble bursts on a free surface (Laurent Duchemin)
A droplet forms at the
tip of the jet, usually an order of magnitude, or approximately ten times smaller
than the initial bubble. It has high velocity and accounts for the tickling sensation
felt when approaching a glass of bubbly liquid with large bubbles (such as some bubbly
natural water brands) to one's face.

Numerical methods and schemes
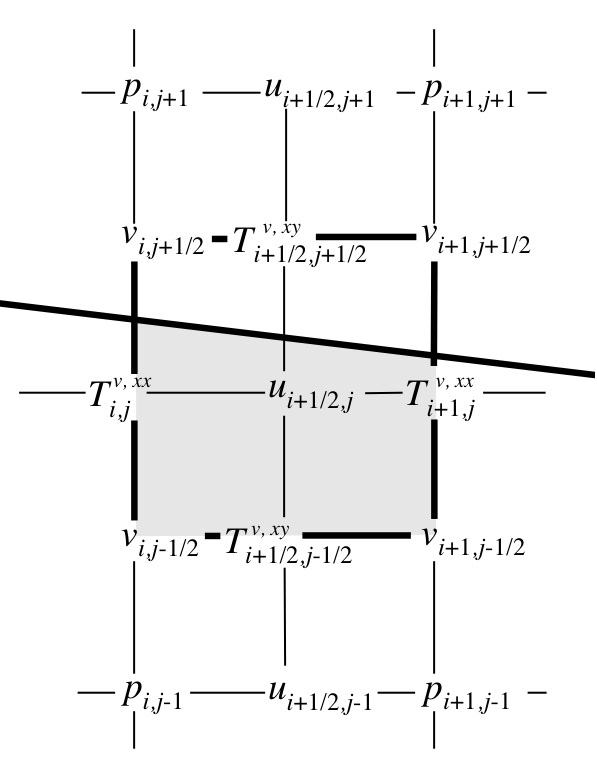
A typical discretization for velocities and
viscous stresses around a cell cut by an interface, extracted from
Tryggvason G., Scardovelli R. and Zaleski S., Direct Numerical Simulations of Gas-Liquid Multiphase Flows, Cambrigge University Press, to appear (February 2011)
. Click on image to enlarge
The main difficulty of numerical methods for the simulation of interfaces is the tracking of a curve or surface on the computational grid. Another difficulty is the discretization of the singular forces involved : surface tension is an obvious example but gravity also creates problems. It can be obtained through
the single equation or immersed boundary method: it amounts to write the
Navier-Stokes equations for the two fluids (liquid and gas) as if there
was only one fluid, but with variable viscosity and density. The surface tension
term is alro added on the grid, using a for instance a weighted distribution on a few neighbouring grid sites.
Volume-of-fluid methods
Our team has developed (see VOF references) an original version of this method (Volume of Fluid/Piecewise Linear
Interface Construction or VOF/PLIC). The original part of this approach
lies in the reconstruction of the interface through non-continuous segment
and to propagate them with a Lagrangian method. It is this Lagrangian
dynamics that differs from other methods through the elementary flux calculation.
In particular, we have shown that the method amounts to an area-preserving mapping of the
computational cells (a geometrical transformation) and that the volume is conserved
to machine accuracy. The scheme
has been tested on different theoretical and experimental standard test cases. Notably,
one obtains a very good agreement with
the capillary wave theory of small amplitudes, which confirms the correct
calculation of the surface tension terms. In addition, the topology changes
are well described in the case of the detachment of a drop by gravity.
Codes for the VOF method have been developped in planar and axisymmetric
geometries in 2D and in 3D, The SURFER
code that has been developped by several DALEMBERT coworkers developed may be found here It is however not maintained anymore apart for some infrequent additions. The Gerris Flow Solver code developped by Stephane Popinet also uses the VOF method.
Front tracking: marker chains
We have also
developed a surface or marker method for interface tracking. Our method is only two-dimensional, but has the advantage of higher accuracy by using third-order splines and a "pressure-correction" methods to improve the computation
of surface tension and remove spurious currents.
(See front-tracking
references and book).
The interface is then reconstructed by splines which
connect virtual marker particles. This method allows a much better
accuracy, for instance for a capillary-wave test case.The
corresponding code may be
found here.
Coworkers
Addresses:
Institut Jean Le Rond d'Alembert
UPMC - Université Pierre et Marie Curie, CNRS, UMR 7190
4 place Jussieu,75005 Paris
tel +33 1 44 27 87 23
email: zaleski (aa tt) ida.upmc.fr
Top of the page
FCIH Group home Page
Institut Jean Le Rond d'Alembert
 Atomization processes involve the development of the instabilities at the interface of
a high-speed jet. The combustion of liquid fuels requires their initial breakup into small droplets. Combustion technology thus provides a powerful incentive to study atomization. Injection devices present in both
petrol and diesel car engines control the atomisation of fuels and thus
the typical droplet size. This eventually
determines the quality of the combustion,
such as engine efficiency or pollution rate. We have
performed numerous calculations
of atomization.
Atomization processes involve the development of the instabilities at the interface of
a high-speed jet. The combustion of liquid fuels requires their initial breakup into small droplets. Combustion technology thus provides a powerful incentive to study atomization. Injection devices present in both
petrol and diesel car engines control the atomisation of fuels and thus
the typical droplet size. This eventually
determines the quality of the combustion,
such as engine efficiency or pollution rate. We have
performed numerous calculations
of atomization.
 Droplet
impacts
Droplet
impacts Bubble
dynamics and other topics
Bubble
dynamics and other topics Numerical methods
Numerical methods


