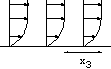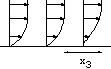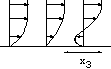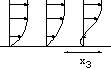
Ecoulements Granulaires Secs avec la Rhéologie du µ(I)


Qu'est ce qu'un matériau granulaire ?
Le sable, le gravier, les roches, mais aussi les céréales, le sucre... sont des exemples de matériaux granulaires de la vie de tous les jours. En revanche un matériau plus petit que 100µm est appelé "poudre", les poudres ont un comportement différent. Constitués de millions  de grains de forme quasi identique, les matériaux granulaires ont la particularité d'exister en "tas" (tas de sable, tas de gravier, tas de blé, tas de patates, terril). Ces tas correspondent à un état immobile des grains, en ce sens ils se comportent comme un objet "solide". Ils ont aussi la particularité de "couler" comme un "fluide": c'est ce qui arrive lors d'une avalanche de cailloux et roches sur le flan d'une montagne, lors d'un effondrement de pâté de sable sur la plage, de l'éboulement d'un fossé, d'une tranchée, de l'écoulement dans un sablier, ou dans un silo de céréales.
un tas de blé (PYL)

Simuler le mouvement de chaque grain
Ces matériaux étant constitués d'un grand nombre de grains, on peut calculer le mouvement de milliers de grains se déplaçant les uns par rapport aux autres et s'entre choquant.  Cette méthode rendue possible par la puissance des moyens de calculs (mais de fait limitée par ceux ci) permet une simulation fine des écoulements granulaires. Plusieurs, méthodes existent, mais la dynamique de contact (J.-J. Moreau, F. Radjai) a notre faveur (exemples d'écoulements par Lydie Staron).

Vision continue des matériaux granulaires, le µ(I)
Mais un autre point de vue existe, il consiste à oublier les grains en regardant d'un peu loin le tas de grains. On parle alors d'approche continue (cette approche est naturelle, en effet, des milieux solides ou fluides tels que l'acier et l'eau sont considérés comme continus alors qu'ils sont constitués d'atomes).  Des approches existent en partant de l'état solide et d'autres en partant de l'état liquide, les deux n'étant pas encore vraiment fusionnées. Mais récemment, une approche appelée rhéologie du µ(I) a été proposée, de manière originale, dans un article collectif synthétisant les travaux communs de plusieurs équipes, signé GDR Midi (un historique du pré-GDR Midi, ).

Lors qu'il est en mouvement, le milieu est tel que ses contraintes normales et tangentielle sont toujours reliées, les contraintes sont à un seuil. En chaque point, la contrainte tangentielle (τ) est égale à un coefficient de friction (le µ) que multiplie la contraine normale (la pression p):  τ = μ p. C'est localement la loi de friction de Coulomb. Mais le coefficient µ est lui même une fonction d'un nombre sans dimension I=d (∂u/∂y)/ √(p/ρ)  qui représente le rapport entre le temps de chute d'un grain et le temps de déplcement de ce grains dans l'écoulement.

Cette théorie a permis de mieux interpréter de nombreux phénomènes physiques de manière à proposer une modélisation mathématique permettant de comprendre de nombreux aspect des écoulements granulaires. L'état actuel de la connaissance est décrit dans l'ouvrage "Les Milieux Granulaires Entre Fluide Et Solide" de B. Andréotti,Y. Forterre & O. Pouliquen


Exemple d'écoulement: Effondrement d'un tas
Jouer sur la plage à démouler un tas de sable d'un seau est un fait analogue (dans une certaine mesure) à essayer de comprendre une avalanche de roches en montagne. C'est pourquoi de nombreuses expériences (initiées par E Lajeunesse) en laboratoire ont été faites sur cette configuration simple de tas de sable ou de micro billes  de manière à prédire l'expansion maximale d'une avalanche. Sur l'image ci contre nous présentons une simulation numérique, à l'aide du solveur Navier Stokes Gerris de l'effondrement d'un tas de grains à différents instant, du pâté initialement relâché au tas final immobilisé. En gris clair et sombre, ce sont tous les grains, en traits rouges, l'approche continue. Les deux dynamiques d'effondrement sont quasi similaires et les tailles des tas finaux ont été comparés aux expériences, l'accord est excellent sur la prédiction de la position de l'excursion maximale du tas en fonction de sa taille initiale.
(l'application immédiate serait de prédire où s'arrête une avalanche compte tenu de la forme des montagnes alentours, bien entendu, nous n'en sommes pas là car l'influence des tailles de roches différentes et surtout des infiltrations d'eau, sont encore des sujets ouverts).




Exemple d'écoulement: Ecoulement dans un sablier
De même que l'étude du tas de sable paraît à première vue relever d'activité de plage, celle du sablier semble aussi dépassée. Il y a bien longtemps que les quarts à bords des bateaux ne sont plus mesurés par des sabliers de demi heure, seuls instruments de mesure du temps en mer lors de la conquête des océans. Cependant, le sablier reste mystérieux, une des grandes interrogations est le fait que son débit de grains à travers l'orifice est indépendant de la quantité de grains restants. Cette observation constitue la loi de Beverloo (Hagen 1852 Beverloo 1961). Sur l'image ci contre nous présentons une simulation numérique, à l'aide de la dynamique de contact et à l'aide du solveur Navier Stokes Gerris de l'écoulement dans un sablier. Les deux dynamiques sont quasi similaires et vérifient la loi expérimentale de Beverloo. L'accord n'est pas parfait, car le milieu continu coule un peu plus vite que le granulaire.

 







Autres liens

voir aussi la page granulaire de FCIH

page d'Olivier  Pouliquen
page morphohydro de Bruno Andreotti & Philippe Claudin
page d'Anne Mangeney
page de Lydie Staron
page Granulaire du FAST
page de LMGC90
page de Ken Kamrin
page de François Chevoir
...

Références

  • L. Staron, P.-Y. Lagrée & S. Popinet "The granular silo as a continuum plastic flow: the hour-glass vs the clepsydra"
    Phys. Fluids 24, 103301 (2012); doi: 10.1063/1.4757390

  • P.-Y. Lagrée L. Staron S. Popinet (2011):
    "The granular column collapse as a continuum: validity of a Navier-Stokes model with a μ(I)-rheology"
    Journal of Fluid Mechanics, pp1-31 , doi:10.1017/jfm.2011.335

    • créé 06/12/12 à jour 12/12
        tas de sable devant Jussieu (PYL)