Par cette modélisation, nous pouvons faire varier indépendamment les différents paramètres caractéristiques du problème : Re (par Nu, son inverse), J (par GB) et Pe (par ALF, son inverse). Cependant, afin d’observer des effets de diffusion visqueuse et de diffusion thermique du même ordre de grandeur, nous fixons Re égal à Pe. On a alors Pr = Pe/Re = 1, ce qui est assez proche de la valeur du nombre de Prandtl de l’air (0.715 à 0°C).
Voici les vitesses axiales en régime stationnaire obtenues pour trois valeurs de J différentes, Re = Pe = 50 étant fixé :

- Figure III.1 : Vitesse axiale en régime permanent pour Re=Pe=50 et J=0.01-

- Figure III.2 : Vitesse axiale en régime pemanent pour Re=Pe=1/J=50 -
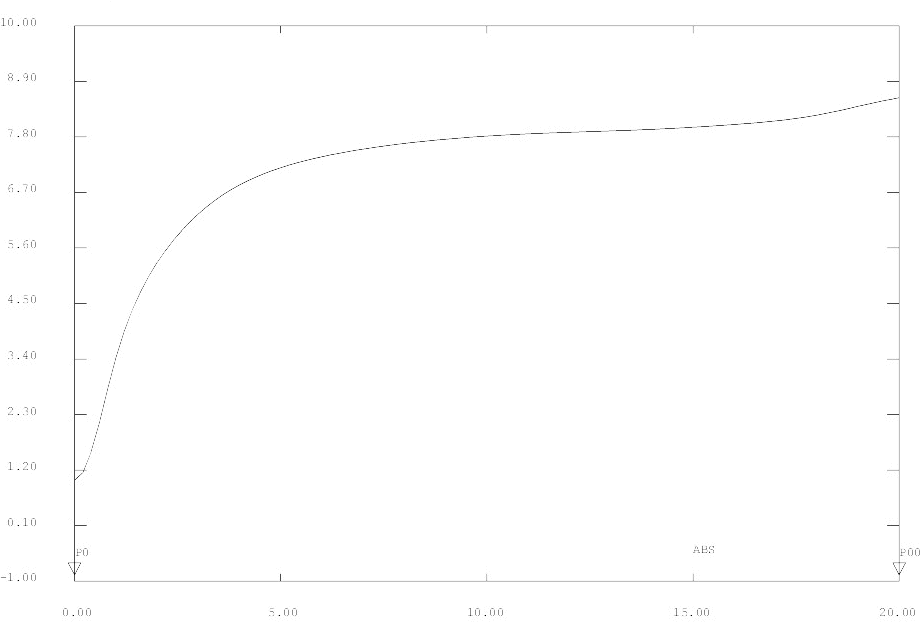
- Figure III.3 : Vitesse axiale en régime permanent pour Pe=Re=50 et J=1 -
On peut alors vérifier la loi de croissance de la vitesse au centre en puissance 1/5 :

- Figure III.4 : Régression en puissance sur la courbe des vitesses axiales -

- Figure III.5 : Régression en a+bx^(1/5) -
On voit que pour J assez grand, la variation de la vitesse sur l'axe en puissance 1/5 de x se vérifie après une phase (intervalle [0,5]) d'adaptation du Poiseuille au panache.
L'étude du cas limite mérite une étude
plus précise. Nous nous attendons en fait à discerner 3
phases pour J suffisamment élevé:
- L'adaptation du profil de Poiseuille à un jet.
- Une évolution de type jet.
- Une évolution de type panache.
Nous avons pu les observer dans le cas Re=Pe=1/J=10 :

- Figure III.6 : Re=Pe=1/J=10 -

- Figure III.7 : Tracé de la courbe de vitesse III.6 en échelle logarithmique -
Avec l'échelle logarithmique, on observe les 3 phases, la croissance en puissance 1/5 pour x assez grand (panache), et une décroissance de jet. Cependant, l'influence du Poiseuille semble encore très importante et on observe une pente de -0.12 et non -1/3. Il faudrait étudier le cas avec une gravité plus faible, en raffinant le maillage pour x faible, ce qui nous fournirait plus de points sur l'échelle logarithmique.