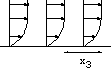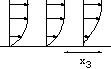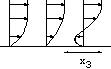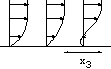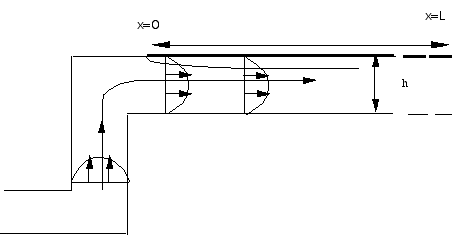
h=5 10-3cm, L=0.24 cm. The channel is very small!

The chemistry in the flow chambers.
Lagrée
P.-Y.
L.M.M. UMR CNRS 7607, Université PARIS VI, FRANCE
www.lmm.jussieu.fr/~lagree/TEXTES/ BIACORE/BIA-Jsb2001.html
c 4/09/01, à jour sept 04; mai 06
What is a flow chamber and what is a BIACORE?
In this page we present
some results on the
chemical reactor used in biological analysis. Those apparatus are
called "flow chamber" or "flux chamber", one of them is the BIACORE
2000 (now 3000!!!).
This machine
has been designed by the company
Biacore.
The flow chambers are commonly used to measure binding rates of
macromolecular interactions with a large area of biological
applications (ADN/ADN, ADN/proteins, polymerisation...).
The measurement is done with reflexion of polarized light ("SPR"
technique see explanation
in french).
Those chambers (such as
the BIACORE device) have been designed to allow the use
of simple kinetic theories (for example, the experimental conditions
are chosen in order to have nearly a constant spatial concentration
on the chip). There are recent studies which show the limits of those
theories: they present more complex theories considering the
coupling between the reaction kinetics and the mass transport. They
permit the understanding of the influence of the mass flux increase
upon the reactions taking place on the wall (the "chip").
 h=5 10-3cm, L=0.24 cm. The channel is very small! |
 |
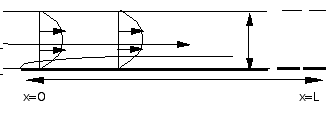
 |
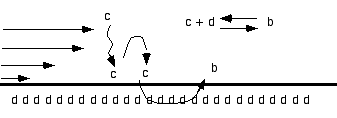 reaction at the wall |
The classical simple kinetic theory as an exact solution: C reacts at the wall with D to give B (with constant of adsorption ka et and desorbtion kd):
kd
C + D <=> B
ka
B'(t) = ka CT (RT -B(t)) - kb B(t) and B(0)=0
where CT is the concentration provided by the flow, RT is the initial concentration of D at the wall. This must be solved for t<tc the injection time, when t>tc, we have dissociation
B'(t) = - kb B(t).
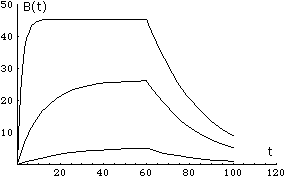
Examples of solutions B(t), here tc=60.
The question is:
what is the influence of the flow on the chemistry?
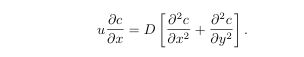
with boundary conditions

but the channel is very thin
so that the equations may be simplified as:

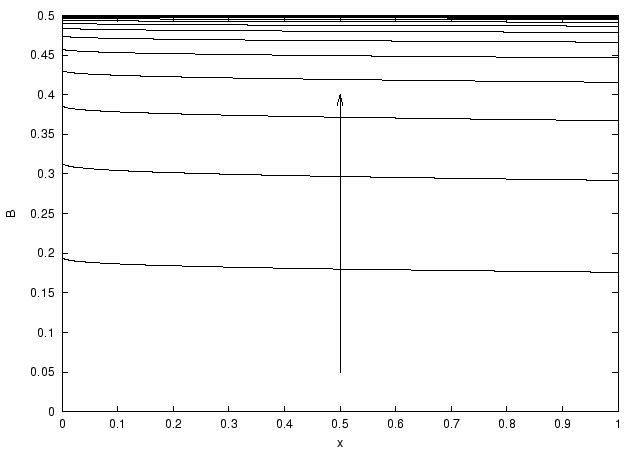
Figure: plot of the concentration of the formed species B(x,t) on the
chip (x between 0 and 1) for various times. We see that there is a
little non uniformity in x. Pe=372, K=1, Da=0.7, DaPe-1/3=0.1
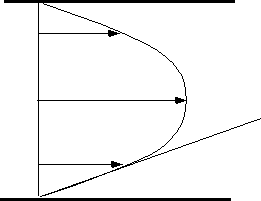
Figure: près de la paroi le cisaillement est
constant.
Figure: tracé de B fonction du temps pour différentes valeurs de Da et Pe, ainsi que la courbe prédite par Edwards.
Les résultats sont confondus pour DaPe-1/3 <.1 (donc la description "Lévêque" marche bien)
Pour DaPe-1/3~.5, l'erreur est de 10%
La solution d'Edwards tombe en défaut pour DaPe-1/3~1
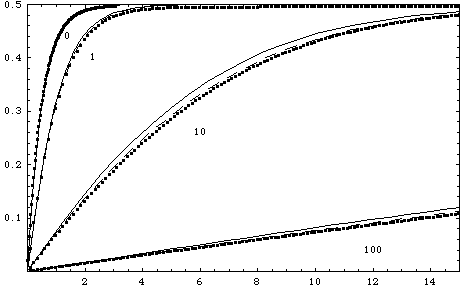
Figure: Réponse de la concentration de ligand formé B(t) en fonction du temps pour K=1, DaPe-1/3=0, 1, 10 et100. Points: résolution numérique du système couplé PDE et ODE, pointillés le modèle intégral avec le coefficient 0.87 (correct pour DaPe-1/3 très petit) et traits: le modèle de Myszka avec le coefficient 0.807 (correct pour DaPe-1/3 très grand, en pratique supérieur à 0.5)
`