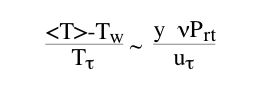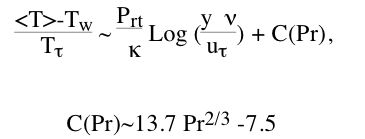| couche limite turbulente |   |
Ecoulement laminaire: exemple Poiseuille

figure Poiseuille
| Stabilité |   |
Landau & Lifshitz (1989) (§26) et citons le: il convient de remarquer que "tout problème concernant l'écoulement de fluide visqueux dans des conditions stationnaires données doit posséder, ne serait ce qu'en principe, une solution stationnaire exacte des équations de l'hydrodynamique"(ce qui n'est pas encore prouvé mathématiquement en 3D). "Or certaines de ces solutions même si elles sont exactes, ne sont pas vérifiées dans la Nature" (N majuscule). "Les écoulements" (sous entendu laminaires) "qui existent dans la Nature doivent être stables: de petites perturbations qui y prennent naissance doivent s'atténuer au cours du temps."
| Notions de "stabilité hydrodynamique" |   |
-Transition:
expérience de Reynolds
tuyau laminaire
Ondes TS


Turbulent / laminaire
Simulation numérique d'une couche limite turbulente
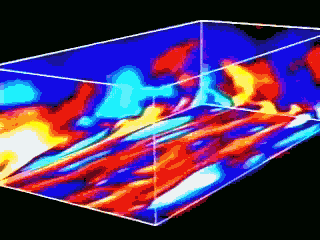
| - Définition de la turbulence |   |
Une définition précise de la turbulence est donc difficile à donner (Tennekes & Lumley (1978) p 1), on peut cependant faire un catalogue:
-l'état turbulent est caractérisé par des variations rapides irrégulières et aléatoires de la vitesse
-les mélanges sont importants et plus rapidement faits que par la diffusivité habituelle.
-le nombre de Reynolds est grand
-l'écoulement est 3D, il est rotationnel.
-l'énergie est dégradée: les écoulements turbulents dissipent l'énergie.
-les échelles mises en jeux ne sont pas celles des échanges moléculaire (le cadre de la mécanique des milieux continus reste valable)
-les caractéristiques sont les mêmes pour tous les fluides (gaz ou liquides), la turbulence n'est pas une propriété du fluide mais seulement un régime particulier.
| Observations expérimentales: |   |

| Observations expérimentales: |   |
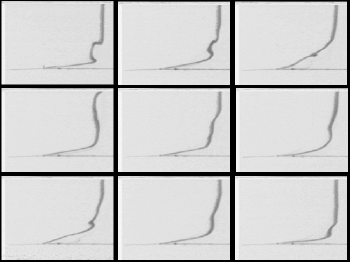
figure quelques profils instantanés de vitesse.
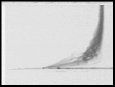
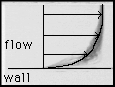
figure superposition: profil moyen.
moyenne (Encyclopedia britannica)
| Observations expérimentales: |   |
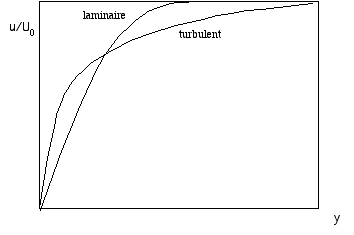
figure profil laminaire et turbulent en unités de couche limite (0.99).
| Le problème de la moyenne des Équations de NS: Équations de Reynolds |   |
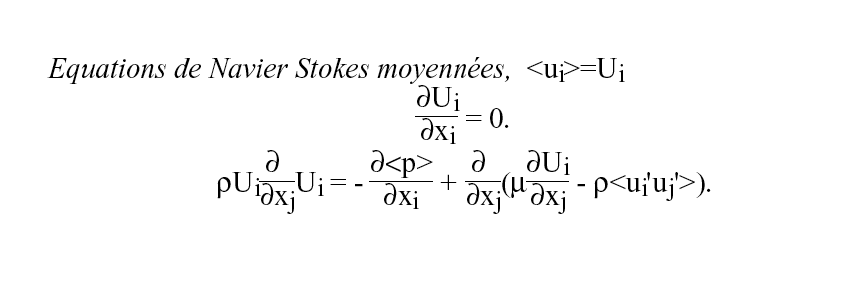
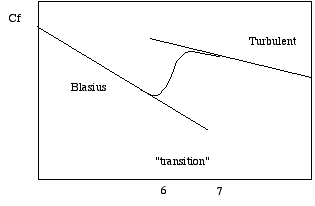
Cf de plaque plane, il varie fortement pour Re entre 105 et 107.
On peut aussi tracer les moyennes des carrés des fluctuations (valeurs "r.m.s." à R~106).
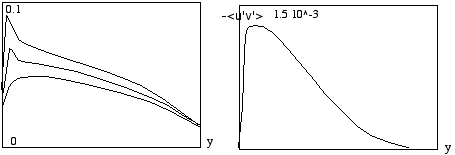
allure typique des fluctuations.
à gauche de haut en bas (<u'2>1/2)/U0, (<w'2>1/2)/U0 et <v'2>1/2/U0. à droite <u'v'>/U02.
sous couche visqueuse --- région log
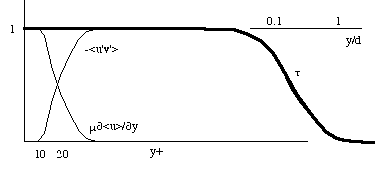
dessin de τ/τp en fonction de la distance à la paroi.
| Loi Log |   |
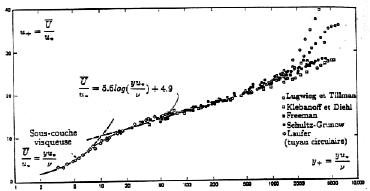
Loi linéaire et loi Log obtenues par compilation de différentes expériences.
<u>/u*= ( u*y/ ν)
pour y+<10
<u>/u*= 2.4 Log(u*y/ ν)+ 5 ou <u>/u*= 5.6 log10(u*y/ν)+ 5.
pour 20< y+<10000
| Couche de défaut |   |
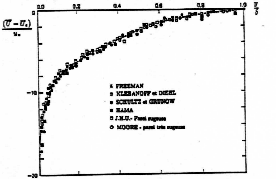
profil universel déficitaire.
(<u>-U0)/uτ = f(y/δ.99).
en pratique:
(<u>-U0)/u* = 5.6 log10( y/ δ) -2.5
u*/U0=δ/L
| Formule du frottement |   |
(<u>-U0)/u* = 5.6 log10( y/ δ) -2.5
et <u>/u*= 5.6 log10(u*y/ν)+ 5. donnent:U0/u*= 5.6 log10(u*δ/ν)+ 7.


U0/u*= 5.6 log10(u*δ/ν)+ 7.
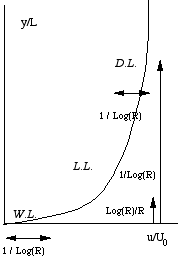
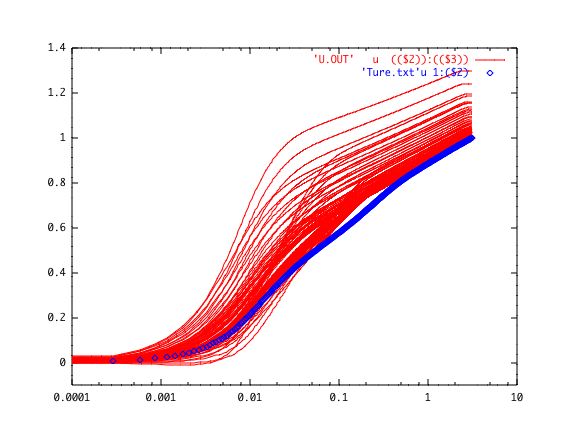
Profil de vitesse turbulente
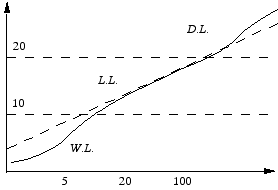
En abscisse u*y/ν, en ordonnée u/u* (échelles Log).
formule de Blasius
Cf = 0.0456 Reδ-1/4.

figure la forme du jet est a peu près indépendante du nombre de Reynolds.

figure L'ouverture (y/x) du jet est constante.


| Equation de la chaleur |   |
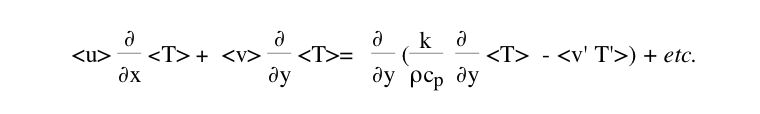
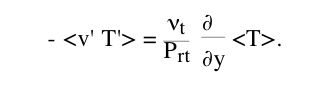
| Equation de la chaleur |   |