http://www.lmm.jussieu.fr/~lagree
Enoncé et corrigé de la PC ENSTA MF204

| PYL
12/10 MF204 http://www.lmm.jussieu.fr/~lagree Enoncé et corrigé de la PC ENSTA MF204 |
PC n°5 Résolution de Poiseuille Turbulent |  |
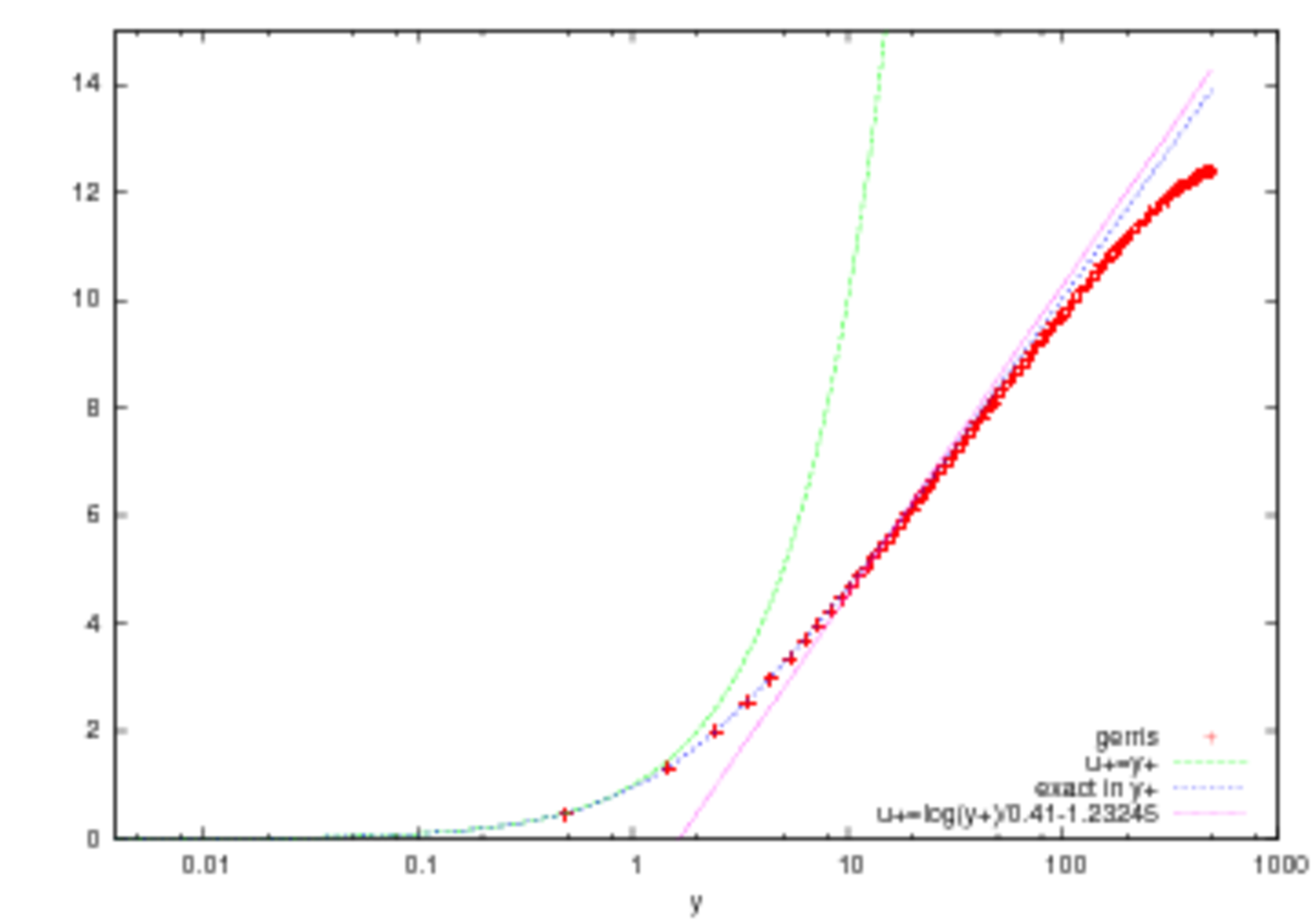
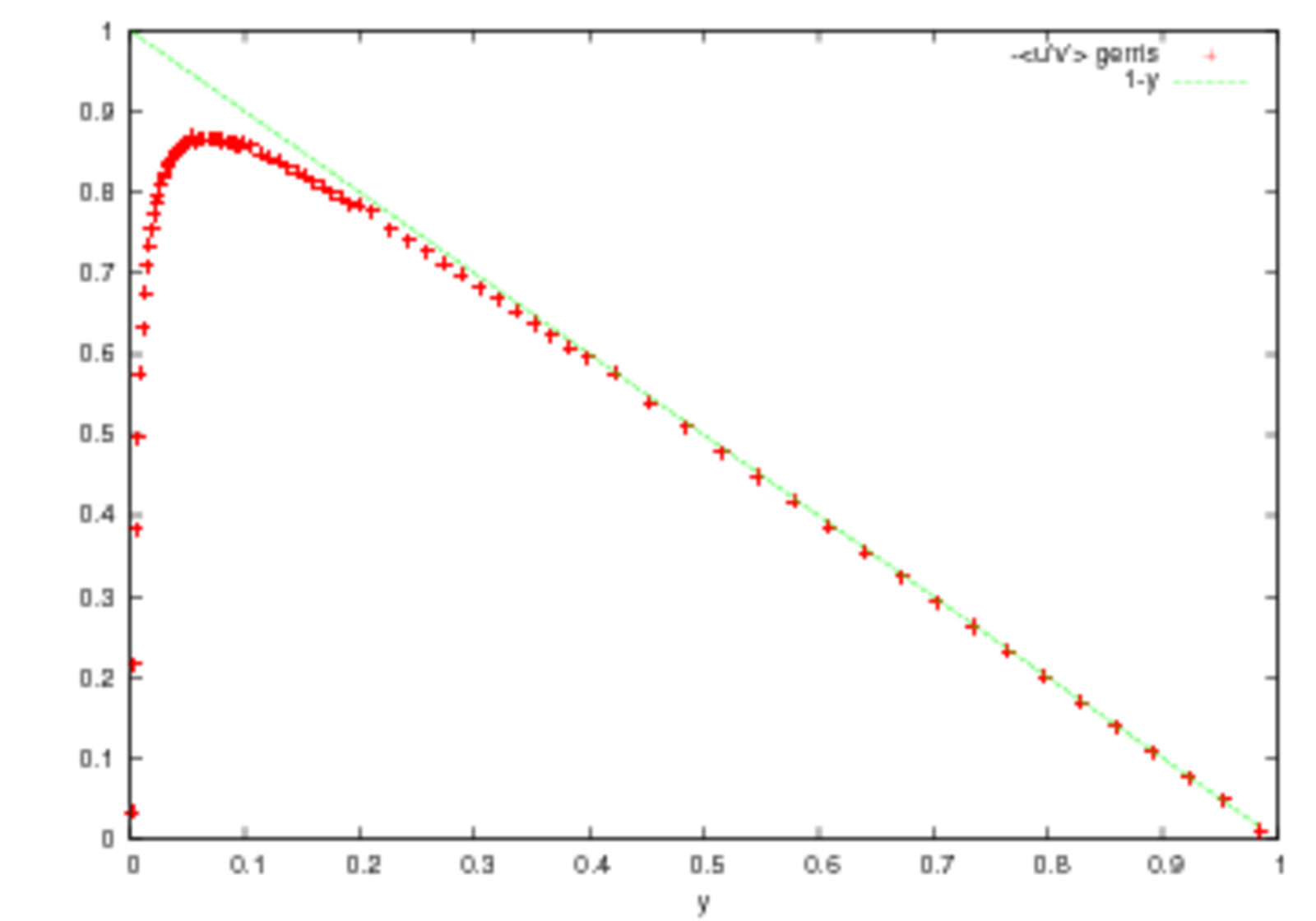
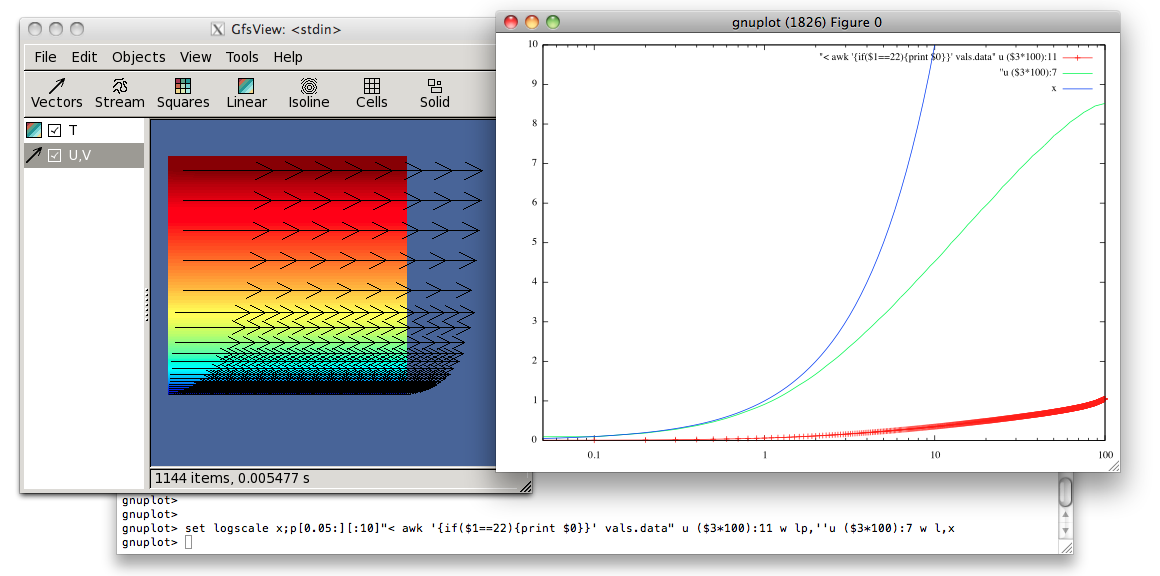
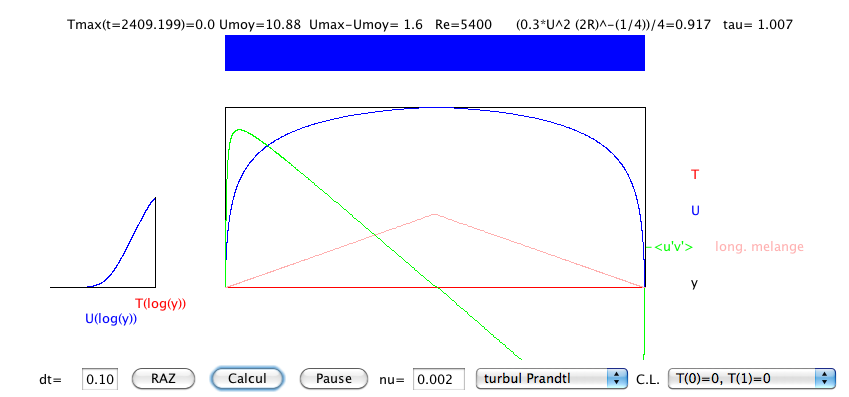
| Le problème de départ est l'écoulement turbulent en 2D entre deux plans infinis distants de 2h. Un gradient de pression pousse le fluide. Les hypothèses de moyenne, d'invariance par translation aboutissent à la résolution de l'équation de Poiseuille turbulent en 2D pour le champ moyen U (et V est toujours nulle), U donnée nulle en y=0, condition de symétrie en y=h. Consulter la Petite Classe pour plus de détails sur les hypothèses, consulter aussi le cours sur les transferts turbulents. | 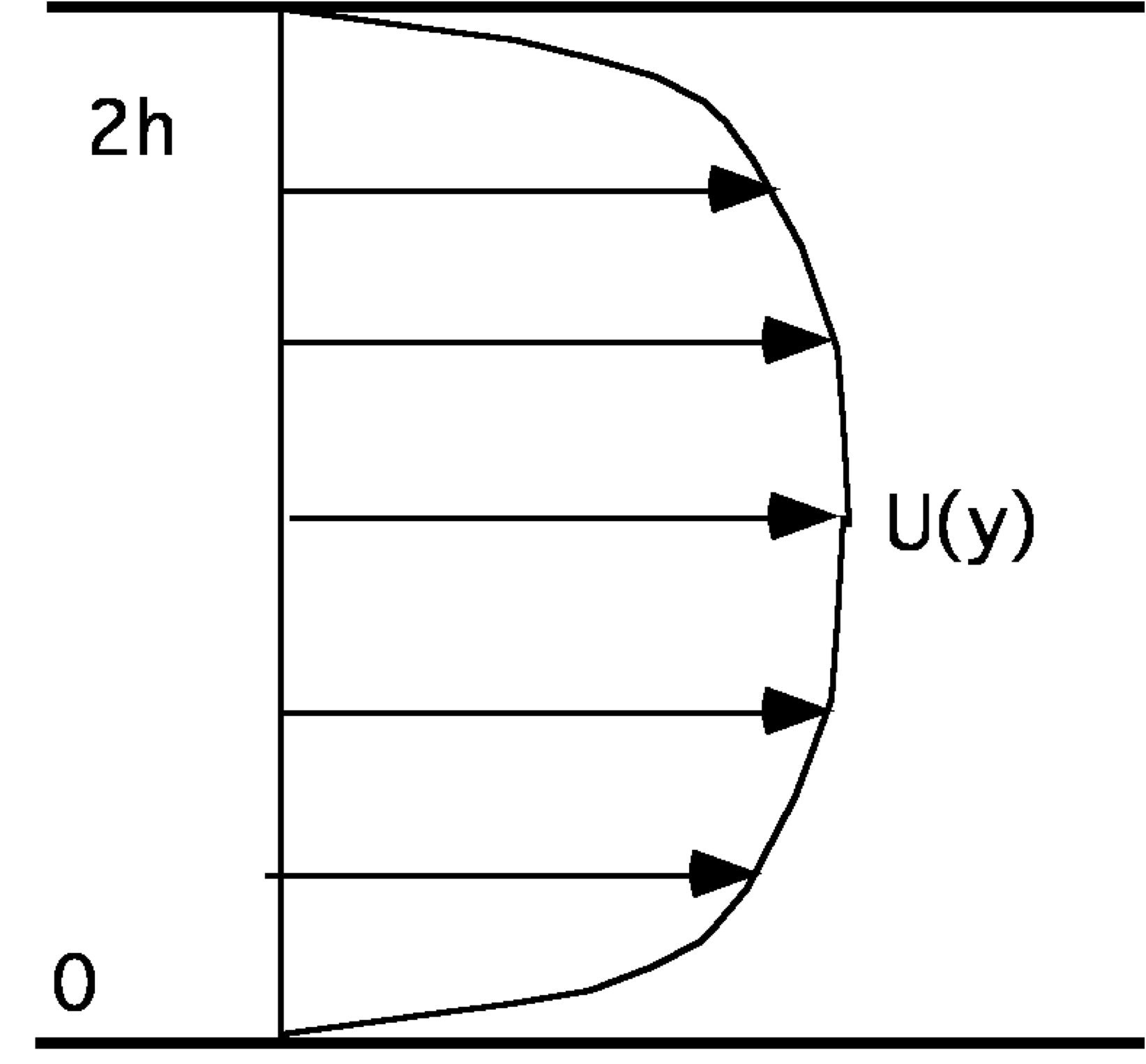 |