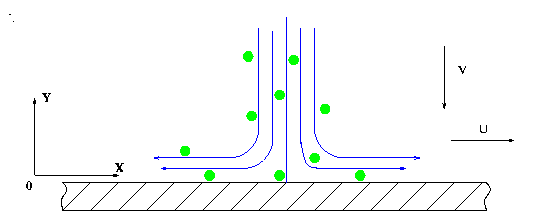
Figure 1: Configuration du problème de point d'arrêt
bidimensionnel
Problématique
La recherche de meilleures performances dans une large gamme de procédés industriels tels que le transport pneumatique, les aérosols, les écoulements diphasiques à bulles, l'utilisation d'ergols métallisés dans les systèmes propulsifs, a conduit la dynamique des fluides diphasiques dispersés à prendre une dimension de plus en plus importante. Dans ce cadre, il est capital, afin d'obtenir numériquement des solutions aux équations de base, d'identifier des conditions aux limites pertinentes. Dans notre thèse, l'objectif est de caractériser de telles conditions dans le cas d'un écoulement près d'une paroi. La méthode utilisée consiste, dans un passage de type microscopique macroscopique, à déduire d'une modélisation au niveau microscopique (lagrangienne) des interactions aux parois pour la phase dispersée, une modélisation macroscopique (eulérienne) des conditions aux limites pour le milieu diphasique global.
Point d'arrêt bidimensionnel

Figure 1: Configuration du problème de point d'arrêt
bidimensionnel
A titre d'étude préliminaire, le problème du point d'arrêt bidimensionnel a été étudié pour un fluide diphasique, composé d'un fluide porteur et d'une suspension de petites sphères solides, arrivant perpendiculairement à une plaque plane infinie. A partir du modèle de Marble, valable dans tout l'écoulement, nous dégageons, après adimensionnalisation et application du principe de moindre dégénéréscence, un système dégénéré permettant l'étude près de la plaque. Les équations de couche limite ainsi obtenues sont résolues numériquement en faisant intervenir le comportement de la phase dispersée à la paroi. Pour la composante normale de la vitesse des particules, la condition à la limite imposée est une faible aspiration à travers la paroi. A l'infini, les conditions aux limites utilisées sont le raccordement de la vitesse tangentielle et de la densité de la suspension. Pour le fluide, on utilise les conditions classiques.
Les solutions numériques obtenues permettent de mettre en évidence un paramètre fondamental : l'inverse du nombre de Stokes de l'écoulement (l), c'est-à-dire le rapport du temps caractéristique de l'écoulement sur le temps de mise en mouvement des particules. Il existe une valeur critique lc de l au delà de laquelle la densité du nuage de particules près de la paroi diverge. Cette divergence, observée par d'autres auteurs, n'est pas physique : elle traduit un défaut de modélisation. Enfin, une étude asymptotique en faisant tendre l'aspiration E imposée à la paroi vers 0 nous a permis de faire apparaitre une dépendance de la valeur critique lc de l en fonction de E. Cette étude, dont l'originalité consiste principalement en l'utilisation de nouvelles conditions aux limites à la paroi, a fait l'objet d'une présentation orale et d'une publication [3].
Modélisation cinétique d'une suspension
En traitant le problème précédent, nous avons vu que le choix d'un débit massique nul à la paroi dans la direction perpendiculaire à celle ci, conduisait à une singularité. Ceci met en évidence, pour un jeu d'équations données, la difficulté d'écrire des conditions aux limites pertinentes. Dans le type de modélisation eulérienne utilisée, il y a donc un défaut de modélisation, tant au niveau des conditions aux limites que des équations. On peut donc penser que la bonne manière de procéder est de développer conjointement les équations et les conditions aux limites par un examen attentif des phénomènes mis en jeu dans un écoulement diphasique comme, par exemple, les collisions particule/particule et particule/paroi.
Aussi, nous avons développé un modèle cinétique, de type équation de Boltzmann, décrivant une suspension de sphères indéformables entrant en collisions non ponctuelles et inélastiques [2]. Pour des sphères faiblement inélastiques et petites devant la longueur caractéristique de l'écoulement, un théorème H a été établi [1] . Avec des hypothèses simplificatrices portant sur les collisions (collisions ponctuelles et/ou élastiques ...) , on retrouve les modèles diphasiques usuels, comme celui de Marble par exemple [5] .
Du fait de la complexité de la structure non linéaire de l'intégrale de collision de l'équation de Boltzmann considérée, il a paru intéressant d'introduire une équation de type BGK [4] . L'équation BGK proposée possède plusieurs propriétés de l'opérateur original, mais ne découle pas rigoureusement de celui-ci. Les difficultés viennent de ce que la dynamique de la collision inélastique de deux particules dans la suspension n'est pas comparable avec celle de deux molécules où les forces d'interaction d'attraction / répulsion jouent un rôle prépondérant. Nous avons choisi un potentiel de type sphères dures, lequel conduit à prendre une fréquence de collision dépendant de la vitesse.
Equations des treize moments
L'équation de Boltzmann, établie dans le cas d'une suspension, permet de construire un système d'équations analogues à celui des équations des 13 moments de Grad. La fonction de distribution des particules est alors approchée par un développement autour d'un état maxwellien. En outre, du fait de l'existence d'un théorème dans le cas de collisions faiblement inélastiques et de particules suffisamment petites, les équations de bilan obtenues pour les premiers moments de la fonction de distribution sont compatibles avec le second principe de la thermodynamique.
D'une loi de rebond caractérisant l'impact d'une particule à la paroi, nous avons déduit un comportement pariétal pour la fonction de distribution puis pour les quantités hydrodynamiques moyennes. Tout d'abord, nous avons pris en compte la dimension des particules. Ainsi, une particule de diamètre D ne peut jamais se situer à une distance inférieure à D/2 de la paroi et les conditions aux limites ont donc été données à cette distance de la paroi. De plus, la collision que nous avons choisie est inélastique, au même titre que celle introduite pour les collisions entre particules. De ce fait, il y a dissipation d'énergie à chaque impact d'une particule à la paroi.
Couche de Knudsen et conditions aux limites
L'analyse de l'équation de Boltzmann sous forme adimensionnelle dans une zone proche de la paroi met en évidence l'existence d'une couche limite dont l'ordre de grandeur est de l'ordre du nombre de Knudsen. L'existence d'une telle couche, dite couche de Knudsen, est classique en théorie cinétique usuelle. Les équations des treize moments ne sont pas valables dans cette couche mais le sont à l'extérieur. Afin d'obtenir des conditions aux limites pour les équations moyennes, il est donc nécessaire d'étudier la couche de Knudsen.
Dans ce but, un modèle cinétique permettant de prendre en compte l'anisotropie et la dissipation induites par le choix de la loi de rebond est introduit. Il utilise une séparation du traitement des particules incidentes et émergentes et est basé sur le modèle BGK proposé précédemment. Il permet alors de déduire de la fonction de distribution pour les particules incidentes, la fonction de distribution pour les particules émergentes ainsi que la fonction de distribution totale, et donc d'obtenir une forme approchée de la fonction de distribution des particules à l'intérieur de la couche de Knudsen.
Une analyse de type couche limite à deux petits paramètres (le nombre de Knudsen et le rapport du diamètre des particules sur la longueur caractéristique de l'écoulement) permet alors d'écrire le raccord des quantités hydrodynamiques moyennes de la suspension à l'intérieur de la couche de Knudsen avec l'extérieur. Nous avons pu ainsi exhiber un jeu de conditions aux limites effectives pour la suspension à la paroi.
Cédric Croizet 2001-05-29