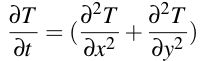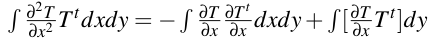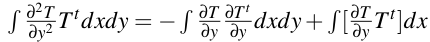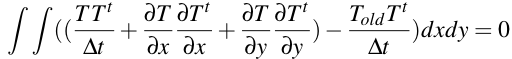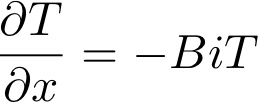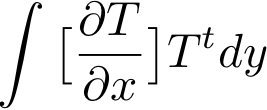PYL 12/2017
PC n°2, la PC1 numérique
texte de la PC
Résolution de l'équation de la chaleur comme dans la PC1
: Température donnée en x=1, adiabatique en x=0 (condition de symétrie), et paroi adiabatique en haut et en bas (ce qui crée une invariance en y).
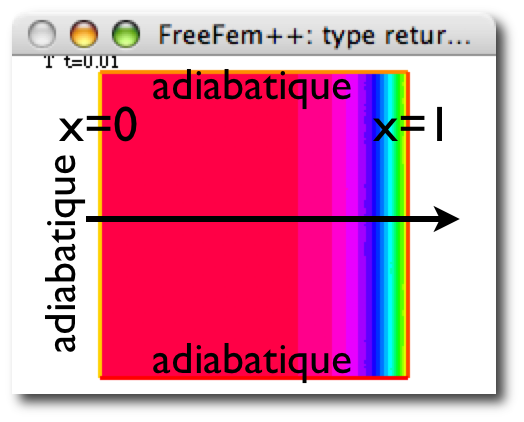
Mise en oeuvre de FreeFem++ dans le cas adiabatique
à gauche, en haut et en bas,
le domaine ci dessus (carré de longueur L0 et de hauteur h0) est codé de la façon suivante:
real s0=clock();
real h0=1; //hauteur domaine
real L0=1.; //longueur
int n=25; //nbre de points
// definition des cotes Maillage
border b(t=0,1) { x= t*L0; y = 0 ; };
border d(t=0,1) { x= L0; y = h0 * t ; };
border h(t=1,0) { x= L0*(t); y = h0 ; };
border g(t=1,0) { x= 0; y = h0 * t ; };
// maillage
mesh Th= buildmesh(b(n)+d(n)+h(n)+g(n));
si on veut voir le maillage, on met, wait=1 signifie qu'il faut attendre CR (Carriage Return) pour continuer
plot(Th,wait=1);
partant de l'équation de la chaleur
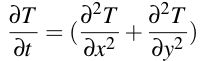
on remplace la dérivée temporelle par l'accroissement de manière à avoir un schéma implicite
òT/òt = (T -Told)/dt
T est l'inconnue du nouveau ps de temps, Told la température connue du pas de temps précédent.
On multiplie par la fonction test Tt et on intègre
par parties (dans les deux lignes suivantes, on a des intégrales
doubles en dxdy et simples sur le contour dy et dx).
Le terme de dérivée seconde en x donne
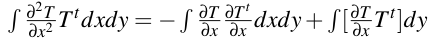
on est adiabatique à gauche la dérivée òT/òx est nulle à gauche,
le terme de dérivée seconde en y donne
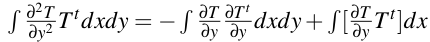
on se donne une dérivée òT/òy nulle en haut et en bas.
le problème variationel final est alors
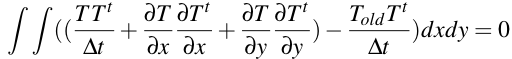
que l'on code sous la forme suivante (avec la condition initiale):
//espace EF
fespace Vh(Th,P2);
Vh T,TT,Told;
real dt = 0.01;
real t=0;
T=1;
Told=1;
problem Ture (T,TT) =
int2d(Th)( T*TT/dt +
( dx(T)*dx(TT) + dy(T)*dy(TT)) )
+ int2d(Th) ( -(1./dt)*(Told)*TT
)
+ on(d,T=0);
on résout ensuite dans une boucle 'tant que' le temps est inférieur à un tmax,
on itère, et on échange Told et T, puis on trace
while((t<2))
{
Ture;
t=t+dt;
Told=T;
plot(T,cmm="T t="+t,T,fill=1,wait=1);
}
on insère une écriture fichier et la comparaison avec la
solution exacte. de la PC 1
Le fichier "pc1_fourierBinf.edp"
contient ce code avec la sauvegarde dans un fichier "NplotT.gp" des
valeurs de y, la température calculée et la
température "exacte" avec 4 modes et enfin le mode 1.
Comme wait=1, il faut faire CR pour passer au temps suivant.
Dans 'NplotT.gp'
il y a par exemple
# vals x T
0 0.705892 0.702199 0.704255
0.04 0.704553 0.700845 0.702866
0.08 0.700541 0.69679 0.698702
0.12 0.693864 0.690045 0.691781
0.16 0.68454 0.680631 0.68213
0.2 0.672594 0.668578 0.669787
... ... ... ...
L'image suivante est obtenue en tappant dans un terminal gnuplot:
gnuplot> p'NplotT.gp' w l,''u 1:3,'' u 1:4
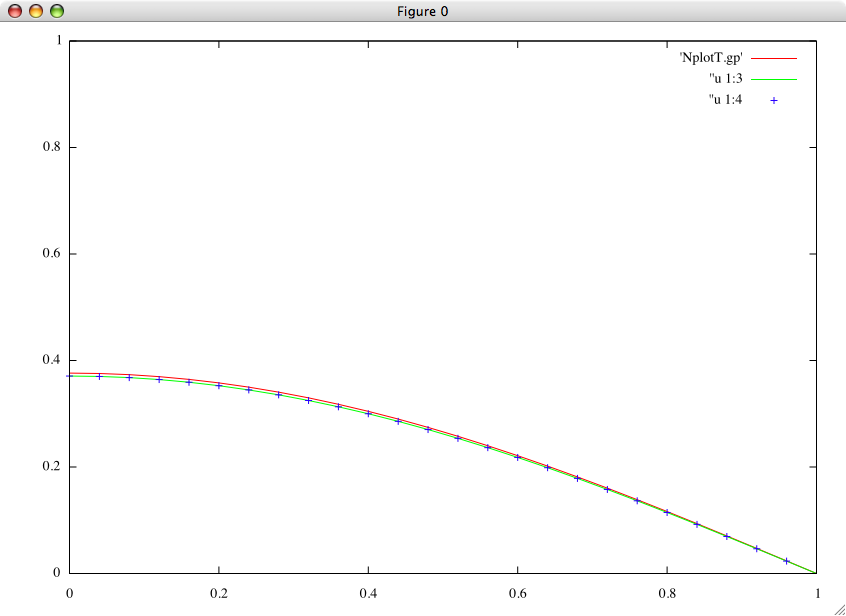
Elle représente le tracé de la deuxième colonne en fonction de la première (u 1:2 est sous entendu),
puis de la troisième colonne en fonction de la première (u 1:3, 'NplotT.gp' est sous entendu),
puis de la quatrième colonne en fonction de la première (u 1:4, 'NplotT.gp' est sous entendu),
Le fichier "pc1_fourierB1.edp"
contient ce code modifié pour tenir compte d'un nombre de Biot
égal à 1 (et un cas à flux constant).
dans ce cas à droite, on a:
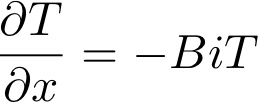
On rajoute donc le terme ((Bi*T)*TT) dans l'intégrale obtenue lors de l'intégration par parties:
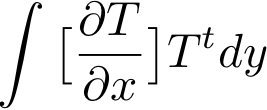
d'ou le code modifié:
real Bi=1;
problem TureBi1P0 (T,TT) =
int2d(Th)( T*TT/dt +
( dx(T)*dx(TT) + dy(T)*dy(TT)) )
+ int2d(Th) ( -(1./dt)*(Told)*TT
)
+ int1d(Th,d) (Bi*T*TT) ;
Plus généralement, si on impose un flux q en sortie on
mettra à la dernière ligne (décommenter les lignes
dasn le code)
+ int1d(Th,d) ((q)*TT) ;
on fera attention au signe.
Dans ce fichier, les images sont suavées en eps et gnuplot est lancé tous les t=1.
le script suivant (eps2gif.sh) permet de convertir en gif animé
#!/bin/sh
#fev 07
#conversion eps en gif anime
rm anime.gif
touch anime.gif
for img in `ls -rt *.eps`
do
convert $img a.gif
echo $img
convert -delay 20 anime.gif a.gif -loop 0 anime.gif
done
gif animé que voici
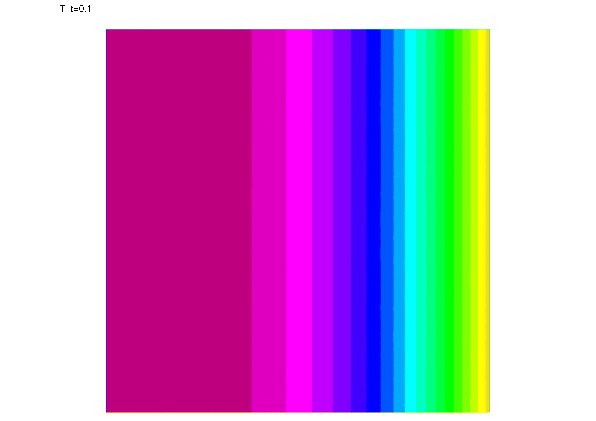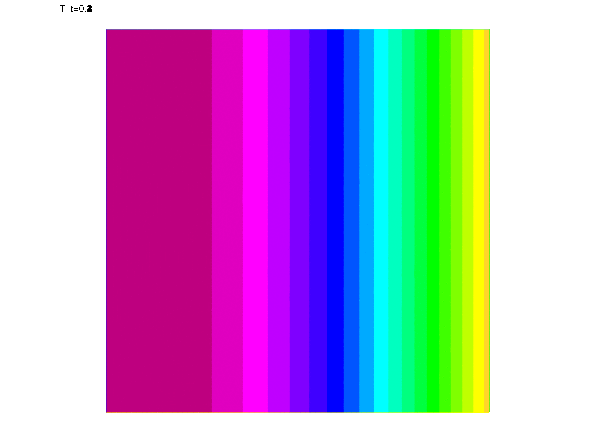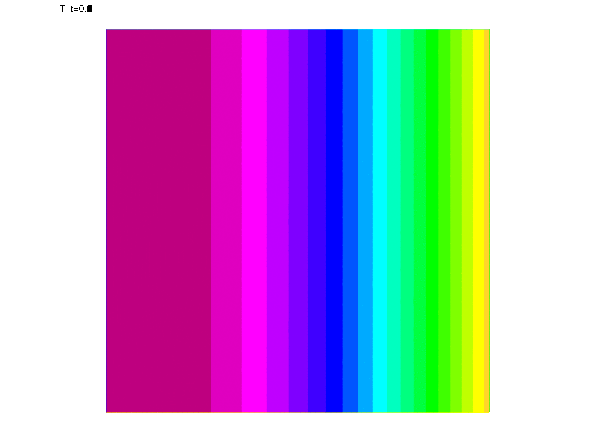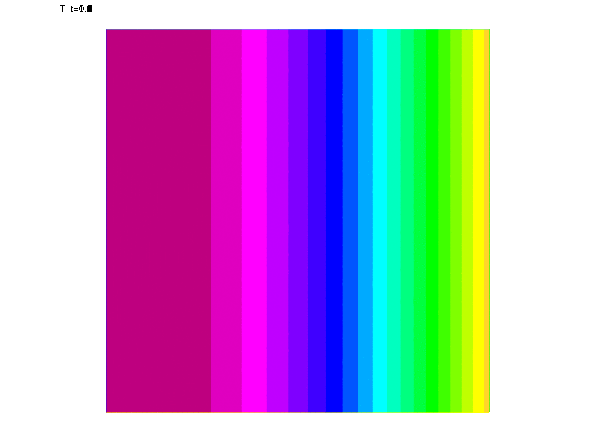
Correction, indications, le fichier "tpc170130.edp"
contient le code fait en PC le 30/01/17
avec la sauvegarde dans un fichier "NplotT.gp" des
valeurs de y, la température calculée et la
température "exacte" avec 1 ou 2 modes. On a comparé aussi avec la solution semblable en erf.
Il y a de nombreux commentaires dans de fichier, les ordres gnuplot sont à la fin en commentaire.
On continue avec un autre exemple, celui de l'ailette
page 2.25 du cours,
faire varier le nombre de Biot, faire varier la forme, etc.
dans le
fichier "ailette.edp"
On continue avec un autre exemple, celui de
l'effet d'entree, solution de Leveque
ou du point d'arret,
Rayleigh Benard, l'instabilité,
Cavité chauffée,